32.Перестановки и размещения

Перестановки. Возьмём n различных элементов: a₁, a₂, a₃,…, a_n. Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения. Каждая из полученных таким образом комбинаций называется перестановкой. Общее количество перестановок из n элементов обозначается P_n. Это число равно произведению всех целых чисел от 1 до n:

P_n = 1·2·3·…·(n-1)·n = n!

Символ n! (называется факториал) - сокращённая запись произведения: 1·2·3·…·(n-1)·n

Пример: Найти число перестановок из трёх элементов: a, b, c.

Решение: В соответствии с приведенной формулой: P₃ = 1·2·3 = 6.

Действительно, мы имеем 6 перестановок: abc, acb, bac, bca, cab, cba.

Размещения. Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, располагая эти m взятых элементов в различном порядке. Полученные комбинации называются размещениями из n элементов по m.

Их общее количество обозначается A_n^m и равно произведению:

A_n^m = n(n-1)(n-2)·…·[n-(m-1)]

Пример: Найти число размещений из четырёх элементов a, b, c, d по два.

Решение: В соответствии с формулой получим:

A₄²=4·3=12

Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.

33.Сочетания

Сочетания

Пусть имеется множество из n различных объектов (элементов), т.е. объекты имеют или разные названия или разные номера. Пусть к < n, к N.

Сочетанием из n элементов по к называется любое подмножество, содержащее к элементов, взятых из данных n элементов без учета порядка выбора элементов. При этом подмножества различаются только элементами, входящими в них; порядок, в котором они расположены, не имеет значения.

Число различных сочетаний из n элементов по к можно найти по формуле:

Пример 5. Из группы в 25 человек нужно выделить 3 человека на дежурство. Сколькими различными способами это можно сделать?

Решение. Исходное множество различных объектов образуют студенты груп­пы. Число всех элементов множества равно 25. Выделенные 3 человека дежурных об­разуют трехэлементное подмножество из общего числа в 25 элементов (n = 25, к = 3). При этом подмножество определяется только элементами, в него входящими, но не их порядком. Поэтому, по определению имеем сочетание из 25 элементов по 3, и по формуле число различных способов выбрать трех дежурных из 25 студентов равно

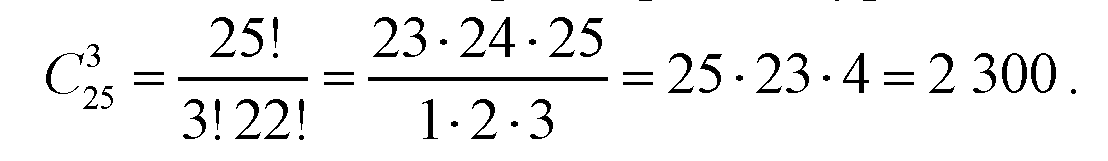
Пример 6. В урне находятся 10 белых, 15 черных, 20 красных шаров. Из урны наудачу берутся 9 шаров. Найдите:

1. сколькими различными способами можно вынуть 9 шаров;

2. сколькими различными способами можно взять 9 шаров, среди которых 6 бе­лых и 3 черных;

3. сколькими различными способами можно взять 9 шаров, среди которых 2 белых, 3 черных и 4 красных шара.

Решение. 1) Всего в урне 45 шаров. Считаем, что шары различимы, например, пронумерованы. Следовательно, имеем множество из n = 45 различных объектов. Наудачу взятые 9 шаров образуют подмножество из к = 9 элементов. Это подмноже­ство определяется лишь элементами, попавшими в него, порядок не имеет значения. Следовательно, это сочетание из 45 элементов по 9:

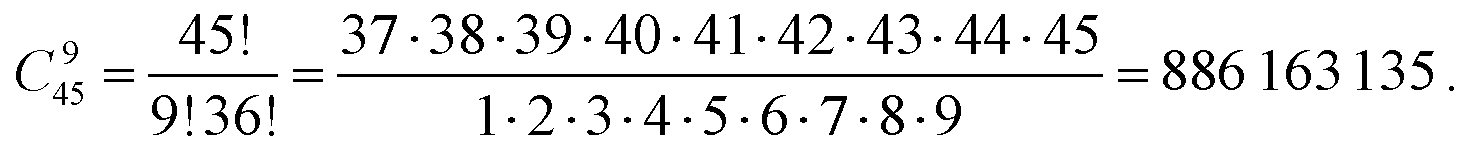
2. Взятие 9-ти шаров, из которых 6 белых и 3 черных, можно разбить на два действия: 1-е действие - возьмем 6 белых шаров из 10 белых шаров, находящихся в урне (это можно сделать С₁₀⁶ различными способами); 2-е действие – возьмем 3 черных шара из общего числа 15 черных шаров (это можно сделать С₁₀³ различными способами). Тогда число различных способов взятия 9-ти шаров нужного состава по правилу умножения равно

3) Чтобы получить 9 шаров, из которых 2 белых, 3 черных и 4 красных, надо последовательно выполнить три действия: а) взять 2 белых шара из общего числа 10 белых шаров; б) взять 3 черных шара из общего числа 15 черных шаров; в) взять 4 красных шара из общего числа 20 красных шаров. Число способов:

Пример 7. В коробке находятся 50 деталей, из которых 10 бракованных. Из ко­робки наудачу берутся 5 деталей. Найдите число различных способов взятия 5-ти де­талей, среди которых ровно 3 бракованных.

Решение. Множество состоит из n = 50 различимых деталей, из которых 10 бракованных, 40 доброкачественных. Чтобы получить множество из 5-ти деталей, содержащих 3 доброкачественные, надо совершить последовательно 2 действия: а) взять три бракованные изделия из общего числа 10 бракованных деталей (это дей­ствие можно совершить С₁₀³ различными способами), б) взять две доброкачественные детали из 40 доброкачественных деталей (это действие можно совершить С₄₀² различ­ными способами). Тогда по правилу умножения оба действия можно совершить: