Дополнительные свойства

Все остальные свойства, присущие рациональным числам, не выделяют в основные, потому что они, вообще говоря, уже не опираются непосредственно на свойства целых чисел, а могут быть доказаны исходя из приведённых основных свойств или непосредственно по определению некоторого математического объекта. Таких дополнительных свойств очень много. Здесь имеет смысл привести лишь некоторые из них.

• Отношение порядка «>» (с противоположным порядком аргументов) также транзитивно.

• Произведение любого рационального числа на ноль равно нулю.

• Рациональные неравенства одного знака можно почленно складывать.

• Множество рациональных чисел является полем (а именно, полем частных кольца целых чисел ) относительно операций сложения и умножения дробей.

 — поле

• В позиционной системе счисления рациональное число представляется периодической дробью. Более того, наличие представления в виде периодической дроби является критерием рациональности вещественного числа.

• Каждое рациональное число является алгебраическим.

25..Множество j иррациональных чисел

Примеры иррациональных чисел:

• √ 2 = 1,41213652..

• √ 3 = 1,730508075..

• (число Пи ) π = 3,14159..

• (основание натурального логарифма ) e = 2,71845..

Обозначается множество иррациональных чисел большой английской буквой [ай] - " I ".

Среди множества чисел иррациональные числа занимают особое место. Они не входят в рациональные числа.

Иррациональные числа ( в отличие от рациональных ) невозможно представить в виде дроби ^a/ _b, где a ∈ Z ( a принадлежит целым числам ), b∈N ( b принадлежит натуральным числам ).

26.Множество r действительных чисел Вещественное число

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Веще́ственное, или действи́тельное число ^[1] — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений ^[2].

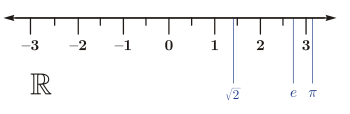
Числовая прямая

Если натуральные числа возникли в процессе счета, рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.

Наглядно понятие вещественного числа можно представить себе при помощи числовой прямой. Если на прямой выбрать направление, начальную точку и единицу длины для измерения отрезков, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять некоторое, и притом только одно, вещественное число. Вследствие этого соответствия термин числовая прямая обычно употребляется в качестве синонима множества вещественных чисел.

Понятие вещественного числа прошло долгий путь становления. Ещё в Древней Греции в школе Пифагора, которая в основу всего ставила целые числа и их отношения, было открыто существование несоизмеримых величин (несоизмеримость стороны и диагонали квадрата), то есть в современной терминологии — чисел, не являющихся рациональными. Вслед за этим Евдоксом Книдским была предпринята попытка построить общую теорию числа, включавшую несоизмеримые величины. После этого, на протяжении более двух тысяч лет, никто не ощущал необходимости в точном определении понятия вещественного числа, несмотря на постепенное расширение этого понятия^[3]. Лишь во второй половине XIX века, когда развитие математического анализа потребовало перестройки его основ на новом, более высоком уровне строгости, в работах К. Вейерштрасса, Р. Дедекинда, Г. Кантора, Э. Гейне, Ш. Мере^[3] была создана строгая теория вещественных чисел.

С точки зрения современной математики, множество вещественных чисел — непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле.

Множество вещественных чисел имеет стандартное обозначение — R («полужирное R»), или (англ. blackboard bold «R») от лат. realis — действительный.