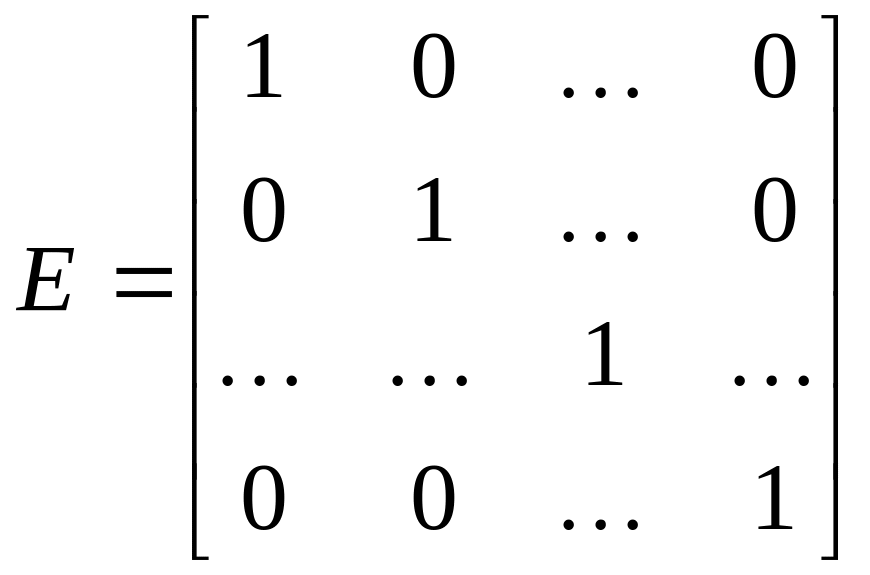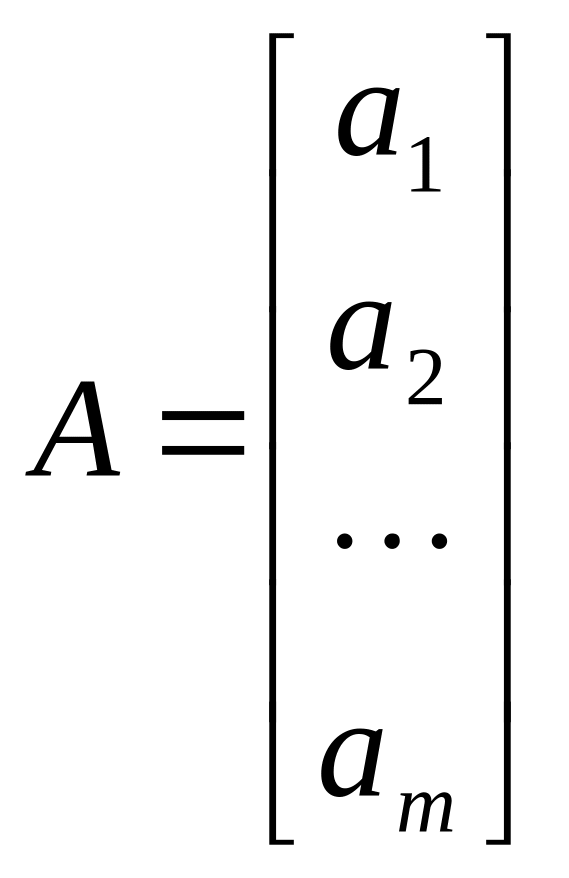Контрольные вопросы
Контрольные вопросы 1
2.Действия над матрицами 4
Равенство матриц 4
Сложение матриц 4
Умножение матрицы на число 4
Произведение матриц 4
3. Сложение матриц 5
4.Умножение матрицы на число 6
5. Произведение матриц 6
6.Транспонирование матриц 7
7.Определители второго порядка и их свойства 7
8.Определители высших порядков 8
9.Свойства определителей 10
10. Обратная матрица 10
11.Элементарные преобразования матриц 12
12.Ранг матрицы 13
13.Свойства ранга матрицы 14
14.Метод окаймления 14
15.Система линейных уравнений 15
16.Решение системы линейных уравнений матричным методом 15
17.Формулы Крамера 16
18.Множества. Основные понятия 18
19.Операции над множествами 20
20.Тождества теории множеств. 22
Свойства 23
Связанные понятия 23
Примеры 23
Счётные множества 23
Несчётные множества 23
Множество рациональных чисел 24
Свойства 24
Основные свойства 24
Дополнительные свойства 26
Вещественное число 27
Позиционные системы счисления 28
Факториальная система счисления 29
В факториальной системе счисления основаниями являются последовательность факториалов , и каждое натуральное число представляется в виде: 29
Фибоначчиева система счисления 29
Непозиционные системы счисления 29
Биномиальная система счисления 30
Система остаточных классов (СОК) 30
Система счисления Штерна–Броко 30
Системы счисления разных народов 30
Единичная система счисления 30
Древнеегипетская система счисления 30
Вавилонская система счисления 31
Алфавитные системы счисления 31
Римская система счисления 31
Система счисления майя 31
Кипу инков 31
Формулы включения-исключения 37
Биномиальные многочлены 40
Биномиальная группа 41
График функции 45
Примеры 45
Способы задания функции 46
Аналитический способ 46
Табличный способ 47
Графический способ 47
Рекурсивный способ 47
Словесный способ 47
Классы числовых функций 48
Свойства функции 48
Общая схема исследования функции и построения её графика 49
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на 2 55
18.Множества. Основные понятия
19.Операции над множествами
20.Тождества теории множеств
21.Множество N натуральных чисел
22.Счетные и несчетные множества
23.Множество Z целых чисел
24..Множество Q рациональных чисел
25..Множество J иррациональных чисел
26.Множество R действительных чисел
27.Системы счисления
28.Правила перевода чисел из одной системы счисления в другую
29.Комбинаторика Правило умножения
30.Комбинаторика Правило суммы
31.Формулы включения-исключения
32.Перестановки и размещения
33.Сочетания
34.Бином Ньютона
35.Функции и их свойства
36.Понятие числовой функции
37.Основные свойства функции
38.Схема исследования основных свойств функции
39.Важнейшие классв функций.Характеристики
40.Сложная функция
41.Корни алгебраических уравнений
1.Матрицы .Основные виды матриц
Прямоугольная
таблица, составленная из
чисел aij,
называется матрицей
размером
.
|
(1.1) |
Числа aij,
входящие в матрицу, называются элементами
матрицы. Горизонтальный ряд чисел
называется строкой, а вертикальный — столбцом
матрицы. Первый индекс i
— номер строки (
),
второй j — номер
столбца (
).
Матрицу принято обозначать заглавными
буквами, например А,
В
и т. д.
Приведем основную терминологию матриц:
|
|
|
|
Если в квадратной
матрице все недиагональные элементы
равны нулю ( |
|
|
|
|
|
|
|
|
|
|
|
),
называется прямоугольной.
),
называется квадратной.
Число ее строк или столбцов называется
порядком матрицы.
)
называется главной
диагональю матрицы
(
).
при
),
то матрица называется диагональной.
