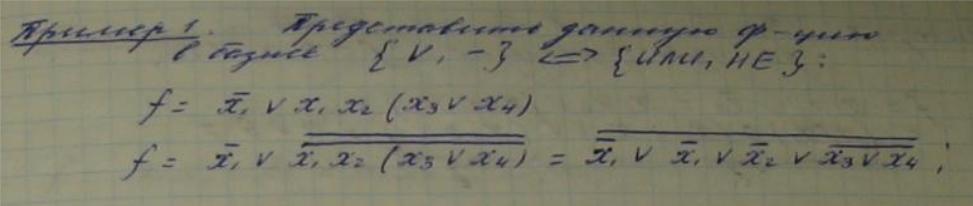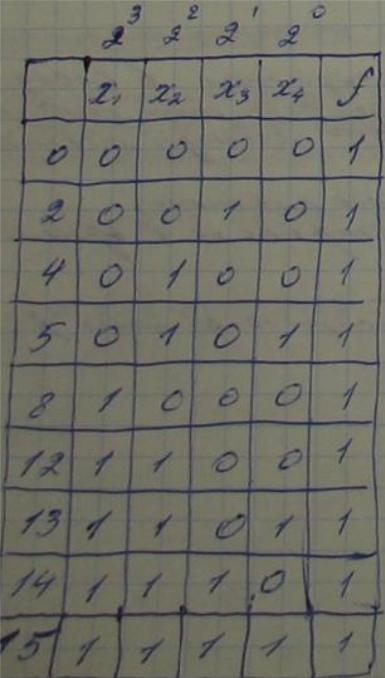
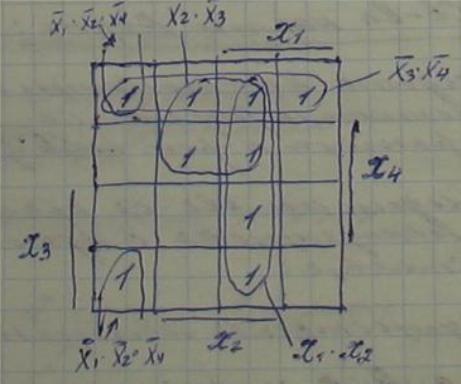
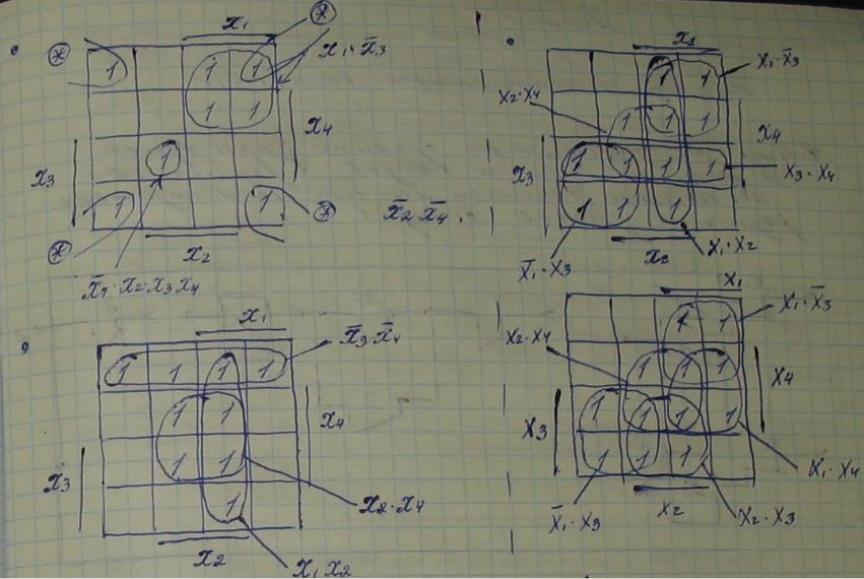
21 .Минимизация фал с помощью карт Карно.
1.
все единицы должны быть заключены в
прямоуг. Контур; 2) во всех клетках
контура должны стоять единицы; 3)число
клеток в контуре равно 2к,
при этом исключается К букв; 4) каждому
контуру соответствует конъюнкция,
составленная из тех переменных, значения
которых не изм-ся во всех клетках контура,
при этом ранг конъюнкции равен N-K;
5) контуры могут накладываться друг на
друга, т.е. иметь общую клетку; 6) контуры,
все клетки к-рого входят в другие контуры
яв-ся лишними; 7) для получения наиболее
простой формулы надо выбирать контуры
с наибольшим числом клеток. Пример:
осуществить мимизацию ф-ции
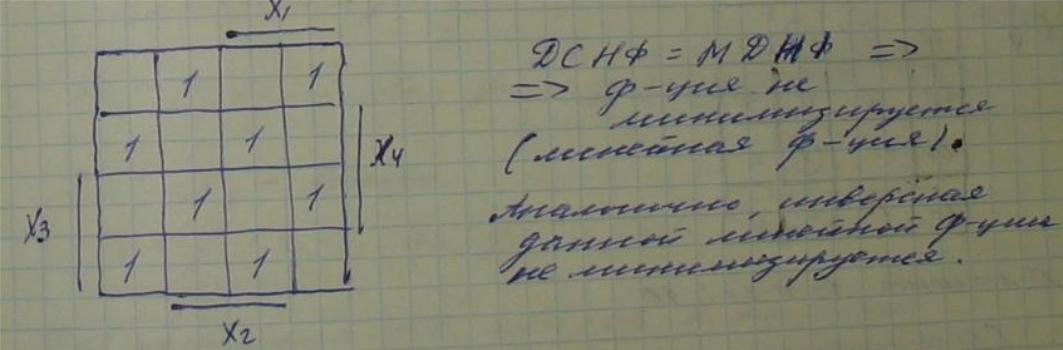
30. Особенные классы фал. Функции, сохраняющие константу 0 и 1. Линейные, монотонные, самодвойственные функции.
2n2, n – число переменных {f1, f2, ….., fn}- замкнутый класс
Классы ФАЛ от двухпеременных
К0 – класс ф-ций, сохраняющих константу 0
f{0, 0, …, 0}=0
Этот класс ф-ций замкнутый
f (x1, …, xn) g(x1, x2, …, xn) x1=g
v(x1, x2, …, xn_=f(g(x1, x2, …, xn), x2, …, xn)
v(0,0,…,0)=f(g(0,0,…,0),0,…,0)=f(0,0,…,0)=0
Доказано, что класс замкнутый.
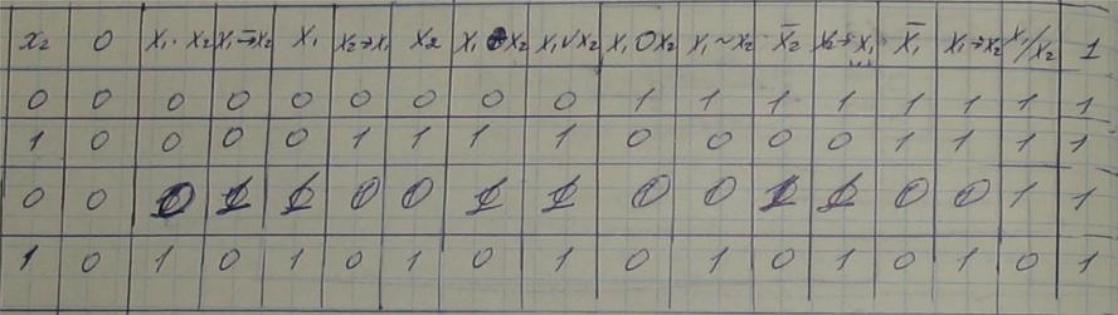
К1 – класс ф-ций сохраняющий константу 1: f(1,1,…,1)=1
K1={x1*x2,
x1,
x2,x1۷x2,
x1~x2,
x2→x1,
x1→x2,1}
К2-класс линейных ф-ций
Линейная ф-ция не мимизируется, т.е МДНФ=ДСНФ
Класс
линейных ф-ций замкнут
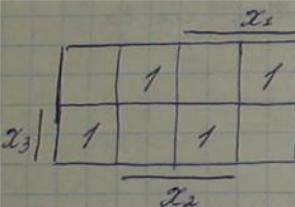
К3-класс монотонных ф-ций а=α1, α2, …, αn b=β1, β2,…, βn
β, α =0 или =1. а≤в, если αi≤βi для всех i 0101< 0111
Ф-ция f(x1,x2,…,xn) – монотонная, если а≤в и f(a)≤f(b)
f(b)=0 – запрещенный набор. Условие монотонности проверяется только для запрещенных наборов.
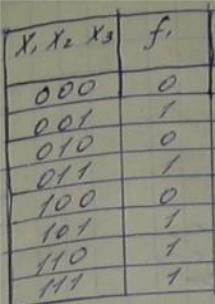
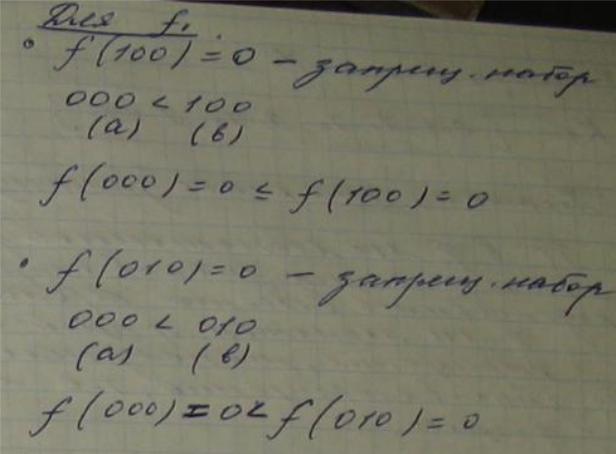
Особенность монотонной ф-ции: МДНФ не имеет переменной с отрицанием
К4-самодвойственные ф-ции. f(x1,x2,…,xn)
f*(x1,x2,…,xn)=
-
двойственная ф-ция
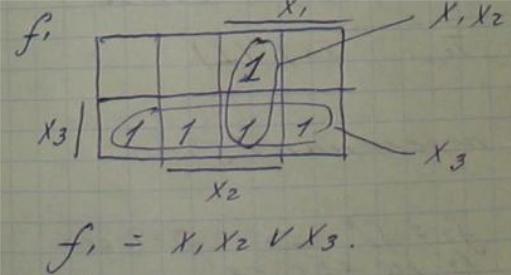
f1=x1x2۷x3
f*1=
-
ф-ция к f1
Двойственная ф-ция получается их
исходной путем замены операции конъюнкции
(умножения) на дизъюнкцию (сложение)
11. Теоремы о том, что функция Вебба и Шеффера образуют базис.
Теорема-ф-ция
Вебба яв-ся базисом. {или,
не}
Докажем данное выражение
1.
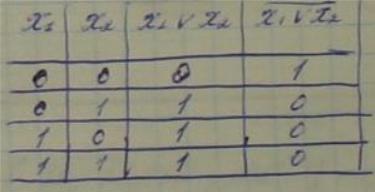2. НЕ: х۷х=х
3.
ИЛИ:
4.
Теорема-ф-ция
Шиффера является базисем х1/х2=
НЕ: x&x=x;
=x.
x/x=x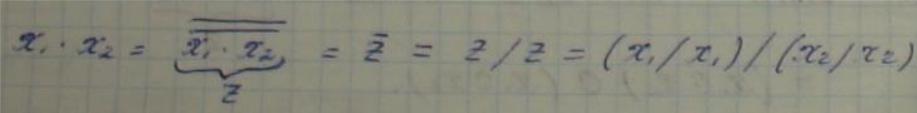
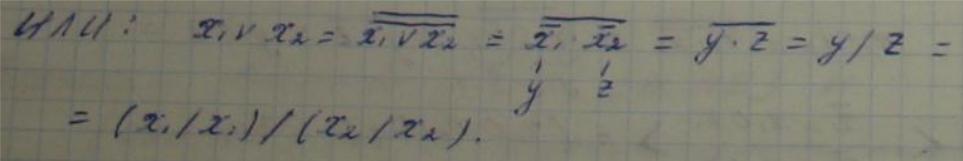
9. Понятие о функционально полных системах фал. Минимальные функционально-полные системы. Доказательство того, что системы (и, или, не}, {или, не}, (и, не} образуют базис.
Система ф-ций {f1,f2,…,fn}есть функционально полная или базис если другая ф-ция может быть получена как суперпозиция данных ф-цуий f1, f2, …, fn
Теорема – набор ф-ций {И, ИЛИ, НЕ}{v,&.-} – яв-ся функционально полным. Система функционально полных ф-ций есть минимальная, если удаление из нее хотя бы дной ф-ции невозможно.
{И,
НЕ} – базис
ИЛИ:
;
{И, НЕ}
{ИЛИ, НЕ}
И:
Теорема
– системы ф-ций {И, НЕ} и {ИЛИ, НЕ} яв-ся
функционально полными
