15.Двоичная и десятичная системы счисления. Перевод из одной системы в другую. Задание фал с помощью десятичных чисел.
Система счисления – совокупность символов и правил для наименования и
обозначения чисел. Символы называются цифрами. Для записи данных в программах на языках высокого уровня используется, в
основном, привычная для человека десятичная система счисления. Преобразование к
двоичному виду выполняется при переводе программы на машинный язык.
двоичная: 0, 1
десятичная: 0,…,9
Преобразования из десятичной системы счисления в десятичную систему.
Выполняется по полиномиальной записи числа (A=an-1Sn-1+…+a1S1+a0S0+a-1S-1+…+a-mS-m )
A[2] = 101.1 = 1*22 + 0*21 + 1*20 + 1*2-1 = 4 + 0 + 1 + 0.5 = 5.5[10]
Преобразования из десятичной системы счисления в двоичную систему.
Преобразование выполняется отдельно для целой и дробной части числа. Все
операции выполняются по правилам десятичной арифметики. Основание новой системы рассматривается как десятичное число. Преобразование целой части выполняется путем последовательного деления целой части на основание новой системы. На каждом шаге вычисляется целая часть и остаток от деления. Остатки и есть значение цифр числа в новой системе счисления. Полученные остатки записываются в новой системе счисления. На первом шаге будет получена
младшая цифра. Процесс продолжается, пока очередная целая часть не окажется меньше основания новой системы счисления. Эта целая часть есть старшая цифра числа.
Пример: 23[10] → ?[2]
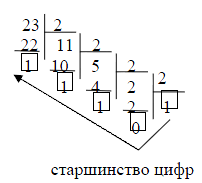
Ответ: 10111[2]
Преобразование дробной части выполняется путем последовательного умножения дробной части на основание новой системы. На каждом шаге выделяется новая целая часть и новая дробная часть. Последовательность целых частей дает значение цифр числа в новой системе счисления. На первом шаге будет получена старшая цифра дробной части в новой системе. Процесс продолжается до получения заданного количества значащих цифр или нулевого значения дробной части.
2. Понятие о ФАЛ. Связь между контактными схемами и предложениями человеческой речи. Особенности ФАЛ. Определение ФАЛ. Область определения и область значений ФАЛ. Функции алгебры логики (ФАЛ) – математический параметр для описания контактных схем (КС). Булевы функции (БФ) = ФАЛ. Между КС и человеческой речью имеется связь. Например: Если стоит хорошая погода (А) и у меня есть свободное время (В), то я иду на охоту (С). Если А и В то С. Каждое предложение может быть истинным или ложным. Истина – 1, ложь – 0. С = f (А, В) – ФАЛ
Конъюнкция «и» - логическое умножение
А |
0 |
0 |
1 |
1 |
В |
0 |
1 |
0 |
1 |
с |
0 |
0 |
0 |
1 |
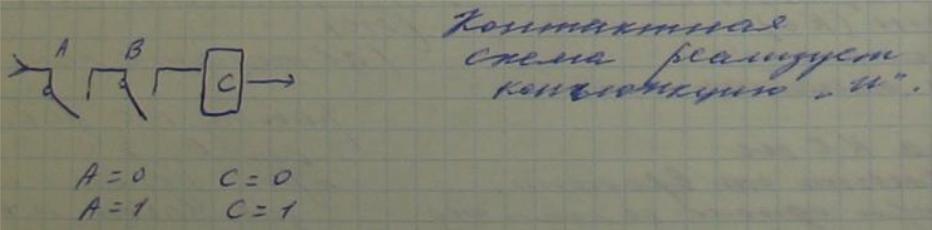
Если А или В то С. Дизъюнкция «или» - логическое сложение
А |
0 |
0 |
1 |
1 |
В |
0 |
1 |
0 |
1 |
с |
0 |
1 |
1 |
1 |
X1 |
X2 |
X3 |
F |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Особенности ФАЛ – 1) переменные и функции принимают только два значения 0 и 1. 2) область задания ФАЛ есть множество двоичных наборов, число которых 2n , n – число переменных.
n=1, 0 1 21
n=2 00 10 2*2=22
11
n=3 000 100
001 101 2*2*2=23
010 110
011 111
3) область значения – множество из 0 и1 {0,1}