34. Поток случайных событий и его основные понятия. Пуассоновский поток и его связь с показательным законом.

Потоком событий называется последовательность событий, наступающих одно за другим в случайные моменты времени. Плотностью (интенсивностью) потока называется среднее число событий в единицу времени

Поток без последействия – если вероятность появления на любом участке того или другого числа событий не зависит от того, какое число событий попало на другие, не пересекающиеся с данным, участки.

Ординарный поток – вероятность появления на элементарном участке ∆t 2х или более событий пренебрежимо мала по сравнению с вероятностью появления 1 события.

Ординарный поток без последействия называется Пуассоновский поток. Если события образуют Пуассоновский поток, то число событий, попадающих в любой участок времени (t₀; t₀+∆t) распределено по закону Пуассона.

, где а- мат. ожидание числа точек, попадающих на участок ; λ(t) – плотность потока. Если λ(t)=const, то Пуассоновский поток называется стационарным или простейшим Пуассоновским потоком. Для простейшего Пуассоновского потока число событий, попадающих на любой интервал длины τ распределено по закону Пуассона а= λτ. Расстояние Т между двумя соседними событиями в простейшем потоке есть непрерывная СВ, распределенная по показательному закону.

35. Гипергеометрическое распределение. Его характеристики.

Гипергеометрический закон – закон распределения случайной величины X, представляющей собой число объектов m, обладающих данным свойством, среди n объектов, случайно извлеченных из совокупности N объектов, М из которых обладают данным свойством.

Параметры распределения: n, N, М. .

36.Нормальный закон распределения. Функция плотности вероятности и ее свойства. Характеристики формы кривой.

Функция плотности

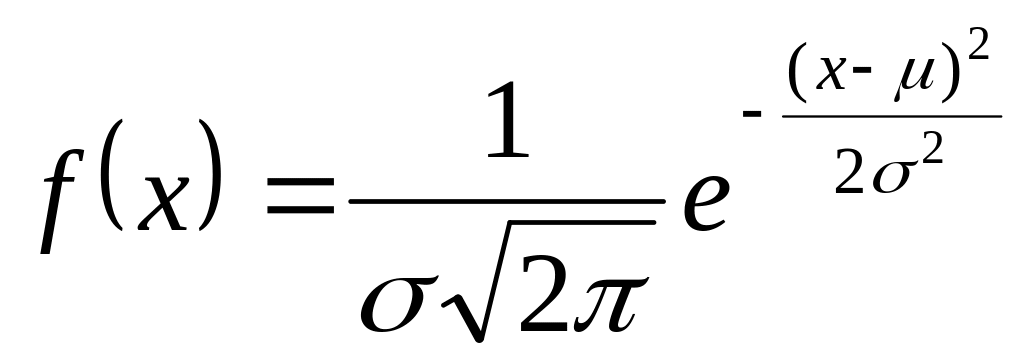
Свойства:

1. f(x)>0 для любого х

2. f(x)0 при х ±∞

3. Функция абсолютно симметрична и унимодальна μ=М(х)=Мо=Ме

4. 2 точки перегиба

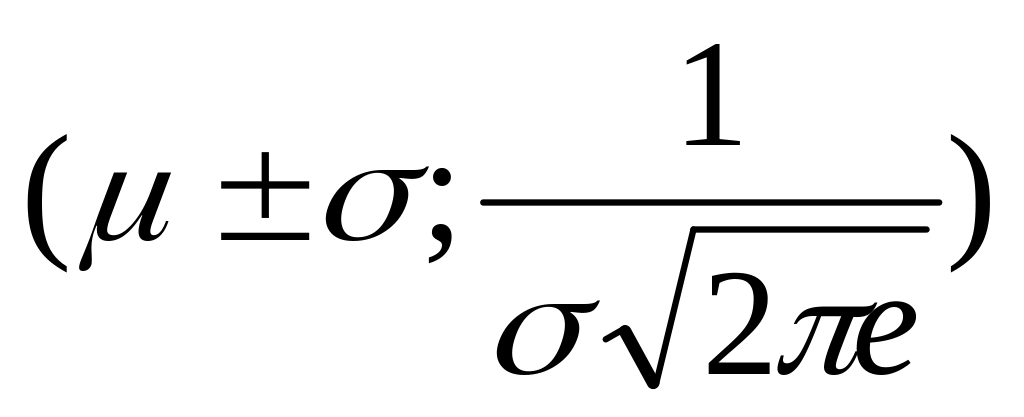
Параметр μ – характеристика положения кривой плотности, координата вершины колокольчика.

Параметр σ – характеристика формы кривой. Чем меньше сигма., тем более вытянутый колокольчик

37. Нормальный закон распределения. Функция распределения, ее вывод через функцию плотности вероятности. Функция Лапласа и ее свойства.

. Замена

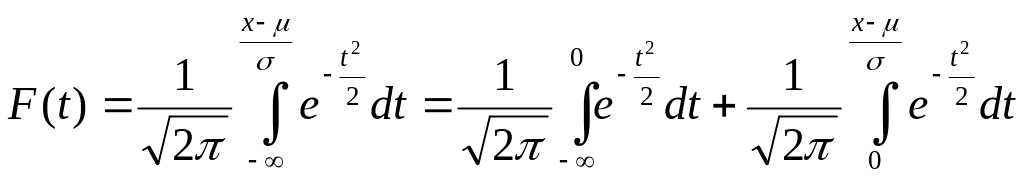
Интеграл Эйлера-Пуассона: => .

Функция Лапласа – =>

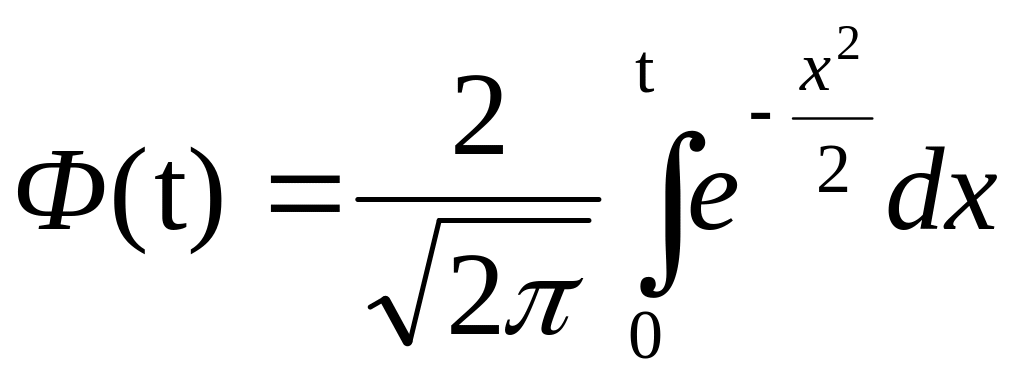Функция Лапласа нечетная.

38. Свойства СВ, распределенной по нормальному закону. Правило 3 сигм.

1) Если Х∈N(μ;σ²), то вероятность попадания СВ Х в интервал от а до b

P(a≤X≤b)=1/2 * [Ф(t₂)- Ф(t₁)] ;

2) Вероятность того, что отклонение СВ от μ не превысит ε>0 по абсолютной величине равна

Р(|x- μ|≤ε)=Ф(t) t= ε/σ

3) Правило 3 сигм. Если СВ Х имеет нормальный закон распределения Х∈N(μ;σ²), то практически достоверно, что её значения заключены в интервале (μ-3σ;μ+3σ) (вероятность выброса 0,0027).

39. Стандартная нормально распределенная СВ. Её свойства.

СНРВ - Х∈N(0;1) (μ=0 ; σ=1)

Свойства:

1) P(a≤X≤b)=1/2 * [Ф(а)- Ф(b)]

2) Р(|x|≤ε)=Ф(ε)

3) Правило 3 сигм. Если СВ Х имеет стандартный нормальный закон распределения Х∈N(0;1), то практически достоверно, что её значения заключены в интервале (-3;3) (вероятность выброса 0,0027).

40. Равномерный закон распределения. Его характеристики (вывод математического ожидания и дисперсии). Функция распределения, её вывод через функцию плотности вероятности.

Вывод функции распределения:

41. Показательный (экспоненциальный) закон распределения. Основные характеристики (вывод мат. ожидания и дисперсии). Функция распределения (без вывода). Связь с пуассоновским потоком. Области применения.

вывод формул для М.О. и дисперсии в приложении

Расстояние Т между двумя соседними событиями в простейшем пуассоновском потоке есть непрерывная СВ, распределенная по показательному закону

42. Показательный (экспоненциальный) закон распределения. Основные характеристики (без вывода). Функция распределения, её вывод через функцию плотности вероятности. Связь с пуассоновским потоком. Области применения.

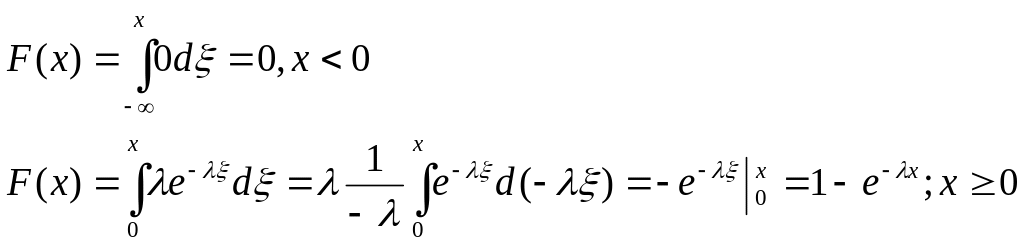
Расстояние Т между двумя соседними событиями в простейшем пуассоновском потоке есть непрерывная СВ, распределенная по показательному закону

43. Логарифмически-нормальное (логнормальное) распределение. Функция плотности вероятности и ее свойства. Функция распределения. Его характеристики. Области применения. Характеристики формы кривой.

С лучайная величина X имеет логарифмическое нормальное (логнормальное) распределение с параметрами μ и σ, если её логарифм (случайная величина lnX) имеет нормальное распределение с параметрами μ > 0 и σ.

Функция плотности вероятностей логнормального распределения имеет вид:

Свойства:

1) Если СВ Х1,…Хn имеют логнормальное распределение, то и их произведение

имеет логнормальное распределение.

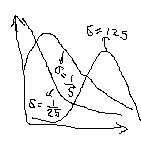
; ; форма кривой

44. Гамма-распределение. Функция плотности вероятности. Его м.о. и дисперсия. Характеристики формы кривой.

- Гамма-функция Эйлера

Г(а+1)=аГ(а) Г(а+1)=а! а- натуральное число.

М(х)=а/b D(x)=a/b²

Экспоненциальное распределение – частный случай Гамма - распределения при а=1 b=λ

При М(х)=1 При а<1 правосторонняя асимметрия.

45. Распределение Пирсона (χ²). Связь с другими распределениями

Функция плотности вероятности. Математическое ожидание и дисперсия.

Если Z₁,Z₂,...,Z_ν – ряд независимых стандартных нормально распределенных величин, то распределение их суммы квадратов называется χ² распределением Пирсона с ν степенями свободы.

М(χ²)=ν D(x²)=2ν

46. Распределение Стьюдента (t-распределение). Связь с другими распределениями. Функция плотности вероятности. М.О. и дисперсия.

Z имеет N(0;1), а величина U² имеет χ² распределение с ν степенями свободы, причем Z и U² независимы. Т имеет t-распределение Стьюдента с ν степенями свободы

М(Т)=0 D(T)=ν/(ν-2) Мо=Ме=М(Т)=0

47. Распределение Фишера-Снедекора (F-распределение). Связь с другими распределениями. Функция плотности вероятности. М.О. и дисперсия.

Пусть и - независимые СВ имеющие χ² распределение с ν₁ и ν₂ степенями свободы.

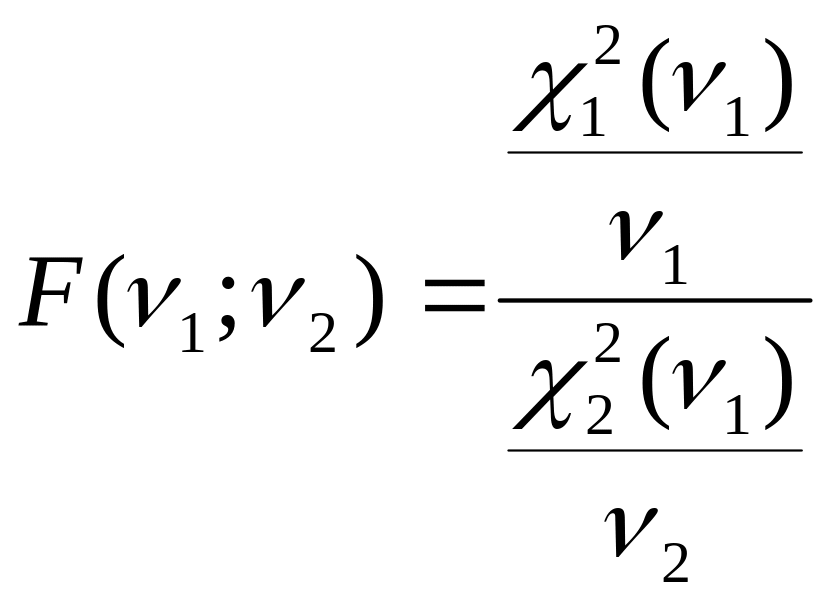
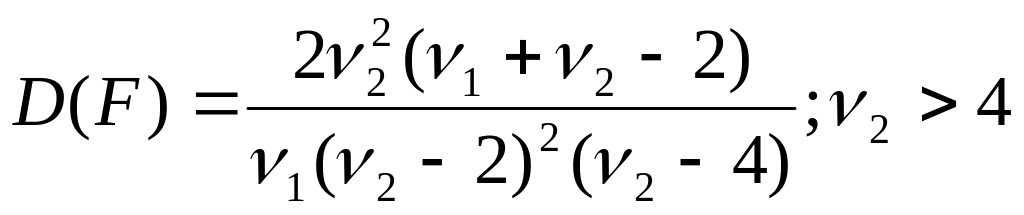
48. Закон больших чисел. Основные теоремы. Лемма Маркова. Неравенство и теорема Чебышёва. Теорема Хинчина. Условия применимости.

В широком смысле под ЗБЧ понимается свойство устойчивости массовых явлений – средний результат действия большого числа случайных явлений практически перестает быть случайным и может быть предсказан с достаточной определенностью. В узком смысле под ЗБЧ понимают совокупность теорем (Бернулли, Пуассона, Чебышёва, Маркова).

З БЧ: Пусть дана последовательность СВ ξ₁,ξ₂,…,ξ_n,…(1). Рассмотрим СВ η_n, являющуюся некоторой заданной симметрической функцией от первых n величин последовательности (1). Если существует последовательность постоянных а₁,а₂,…,а_n , что при любом ε>0

то говорят, что последовательность (1) подчиняется ЗБЧ с заданными функциями f_n.

Лемма (неравенство) Маркова: Если СВ Х не принимает отрицательных значений и у нее существует мат. ож. М(х), то для любого τ>0 выполняется Р(х≥τ) ≤ М(х)/τ Р(х<τ) ≥ 1 - М(х)/τ .

Доказательство: Пусть Х – СВ с плотностью распределения f(x), х≥0. Тогда . Т.к. τ>0

. Т.к. х≥τ, то . Т.к. М(х)>0, то Р(х≥τ) ≤ М(х)/τ

Неравенство Чебышёва: Для любой СВ Х имеющей М.О. и конечную дисперсию, при каждом ε>0 имеет место неравенство Р{|x-M(x)|>ε} ≤ D(x)/ε². Р{|x-M(x)|≤ε} ≥ 1 - D(x)/ε².

Доказательство: По лемме Маркова (для Y≥0): Р(у≥τ) ≤ М(у)/τ. Возьмём У=(Х-М(х))² и τ=ε²

.

Теорема Чебышева: Если Х₁,Х₂,…,Х_n,… - последовательность попарно независимых СВ, имеющих конечные дисперсии, ограниченные одной и той же постоянной С, т.е. D(x_i)≤C, то для любого ε>0

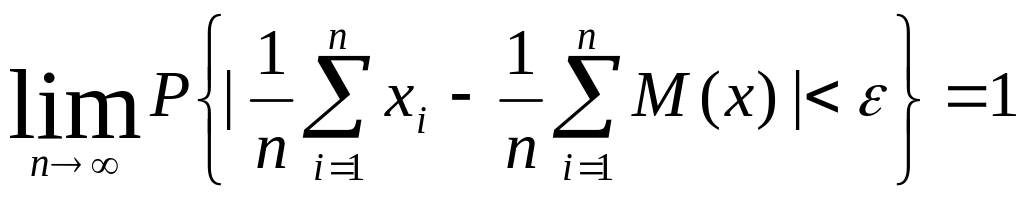
Доказательство:

. Т.к. Р не может быть больше 1, то неравенство выполнено как равенство.

Теорема Хинчина. Если Х₁,Х₂,…,Х_n,… - последовательность независимых в совокупности и одинаково распределенных СВ, имеющих конечное М.О. М(х), тогда каково бы ни было ε>0