1.4. Инвариантные свойства параллельного проецирования

Геометрические фигуры в общем случае проецируются на плоскость проекций с искажением. Проекции не сохраняют линейные и угловые величины оригинала. Характер искажений зависит от положения геометрической фигуры в пространстве, от аппарата проецирования и от положения плоскости проекций.

Однако некоторые геометрические свойства фигур остаются неизменными в процессе проецирования. Такие свойства геометрических фигур называются независимыми или инвариантными для данного аппарата проецирования.

Рассмотрим основные инвариантные свойства параллельного проецирования.

1. Проекция точки есть точка

Это очевидно из самого определения проекции как точка пересечения проецирующей прямой с плоскостью.

2. Проекция прямой есть прямая (рис. 1.6)

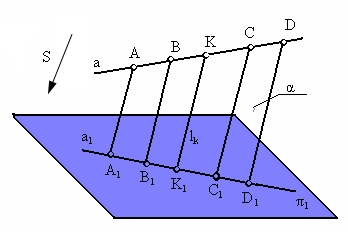
Рис. 1.6. Инвариантные свойства 2, 3, 4

Все проецирующие прямые, проходящие через точки прямой а параллельно направлению проецирования S, образуют проецирующую, или лучевую, плоскость .

Проекция прямой а на плоскость ₁ определяется как линия пересечения этой лучевой плоскости  с плоскостью ₁, т. е. прямая

3. Если точка К принадлежит прямой а, то и проекция этой точки

принадлежит проекции прямой (рис. 1.6)

Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.

Если точка К принадлежит прямой а и плоскости , то и проецирующий луч l_К принадлежит плоскости . Следовательно, этот луч пересечет плоскость ₁ в линии пересечения плоскостей  и ₁, т. е. в точке К₁, принадлежащей проекции прямой а₁.

4. Если точка К делит отрезок АD в отношении m : n то и проекция

этой точки делит в таком же отношении проекцию этого отрезка (рис. 1.6):

Фигура ADD₁A₁ – трапеция. Прямая КК₁ параллельна основаниям трапеции АА₁ и DD₁, следовательно делит ее стороны АD и А₁D₁ на пропорциональные части.

5. Проекция точки пересечения прямых есть точка пересечения проек

ций этих прямых (рис. 1.7)

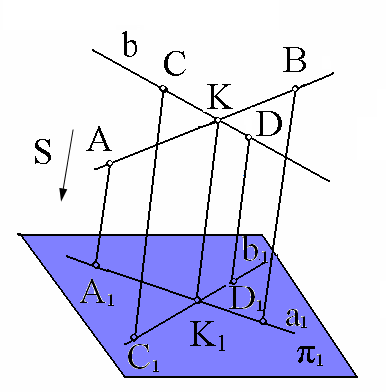
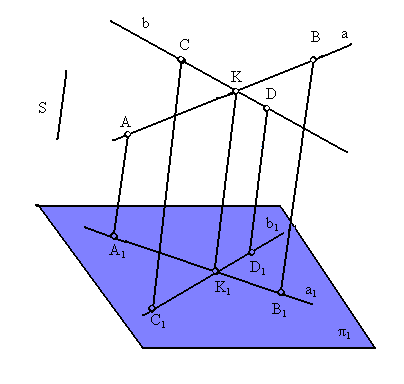
Рис. 1.7. Пример инвариантного свойства 5

Действительно, точка К принадлежит одновременно прямым АВ и CD. По третьему инвариантному свойству проекция этой точки К₁ должна принадлежать проекциям этих прямых, т. е. должна являться точкой пересечения этих проекций.

6. Проекции параллельных прямых параллельны (рис. 1.8)

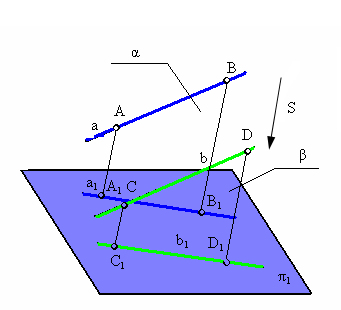
Рис. 1.8. Пример инвариантного свойства 6

Лучевые плоскости  и , проходят через параллельные прямые АВ и CD. Они параллельны, т.к. две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости (АВ CD и АА₁ СС₁). Но две параллельные плоскости пересекаются с третьей по параллельным прямым, следовательно, А₁В₁ С₁D₁.

7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.

И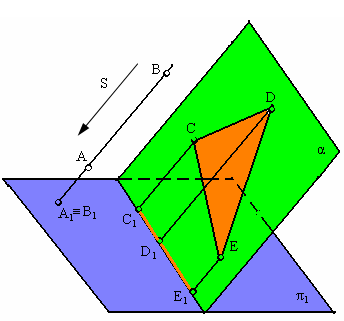 сключение составляет многоугольник (плоская ломаная или кривая линия) расположенный в проецирующей (лучевой) плоскости. Такой многоугольник проецируется в прямую линию (рис. 9).

Рис. 1.9. Примеры инвариантных свойств 7, 8

8. Прямая, параллельная направлению проецирования, проецируется в точку (рис. 1.9)

9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре (рис. 1.10).

Следствия этого инвариантного свойства следующие:

1. Проекция отрезка прямой, параллельной плоскости проекций,

конгруэнтна и параллельна самому отрезку (рис. 1.10):

2. Проекция угла, стороны которого параллельны плоскости проекций,

конгруэнтна этому углу (рис. 1.10)

Рис. 1.10. Пример инвариантного свойства 9 (следствия инвариантных свойств)