3. Нелинейные резистивные цепи
Цель работы. Изучение методов графического анализа, аппроксимации характеристик и расчета гармонических составляющих отклика нелинейных резистивных цепей.
3.1. Описание исследуемых цепей
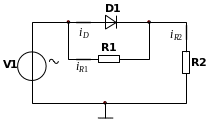
В работе исследуется две цепи – цепь (а) и цепь (б), схемы которых приведены на рис 3.1. Схема исследуемой цепи быстрее всего может быть получена путем преобразования (и переименования) схемы на рис. 1.5 (файл D.ms10). Исследуемые цепи содержат следующие элементы: V1 – независимый источник гармонического напряжения; D1 – диод; R1 и R2 – резистивные элементы. Параметры элементов указаны в табл. 3.1.
а) |
б) |
Рис. 3.1. Схемы нелинейных цепей
Таблица 3.1
Параметры элементов нелинейных цепей
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Параметры элементов |
Рис 3.1 |
а |
б |
a |
б |
а |
б |
а |
б |
R 1, кОм |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
|
R 2, кОм |
1 |
0,5 |
2 |
1 |
4 |
8 |
3 |
6 |
|
IS, А |
10 – 6 |
10 – 6 |
10 – 8 |
10 – 8 |
10 – 9 |
10 – 9 |
10 – 7 |
10 – 7 |
|
N |
1 |
1 |
1,4 |
1,4 |
1,6 |
1,6 |
1 |
1 |
|
3.2. Методические указания к выполнению домашнего задания
3.2.1. Графоаналитический метод анализа нелинейных цепей
Рассмотрим метод определения передаточных характеристик исследуемых цепей с помощью уравнений электрического равновесия и графических построений. Передаточная характеристика нелинейной цепи – это зависимость выходного напряжения цепи от входного напряжения u 2 = f (u 1) (для цепей, приведенных на рис. 3.1, u2 = uR2, u1 = uV1).
Основная система уравнений электрического равновесия (ОСУ) цепи (а) имеет вид:
Исключив из ОСУ мгновенные значения токов, получим уравнения напряжений ветвей цепи (а):
Далее с помощью среды MATHCAD можно составить программу расчета передаточной характеристики цепи (а) (рис. 3.2)*.
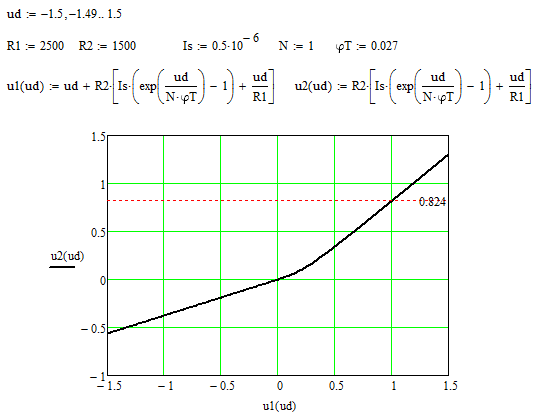
Рис. 3.2. Программа расчета и график зависимости u 2 = f (u 1) цепи (а)
Из ОСУ цепи (б) можно получить уравнения напряжений ветвей этой цепи:
и затем составить программу расчета передаточной характеристики цепи (б) (рис. 3.3).
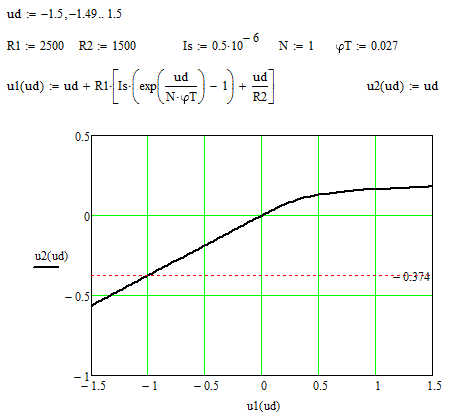
Рис. 3.3. Программа расчета и график зависимости u 2 = f (u 1) цепи (б)
3.2.2. Аппроксимация табличной зависимости
Для аппроксимации зависимости u2 = f (u1) сначала необходимо получить таблицу значений {u1 k , u2 k}, k = 1, 2, ..., N (N – количество точек). Значения {u1 k , u2 k} необходимо определять из графика передаточной характеристики с тремя-четырьмя точными значащими цифрами (см. рис. 3.2 или рис. 3.3).
Коэффициенты аппроксимирующей функции (полинома) определяют методом наименьших квадратов (МНК) или методом выбранных точек (МВТ) с помощью приведенных ниже программ на языке MATHCAD. Графики экспериментальных и аппроксимирующих функций приведены на рис. 3.4.