Тяготение

Закон всемирного тяготения. Эквивалентность инертной и гравитационной масс. Принцип эквивалентности гравитационных сил и сил инерции.

Все тела в природе взаимно притягивают друг друга. Закон, которому подчиняется это притяжение, был уста­новлен Ньютоном и носит название закона всемир­ного тяготения. Согласно этому закону сила, с ко­торой два тела притягивают друг друга, пропорциональна массам этих тел и обратно пропорциональна квадрату расстояния между ними:

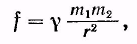(9.1)

где у — коэффициент пропорциональности, называемый гравитационной постоянной. Направлена сила

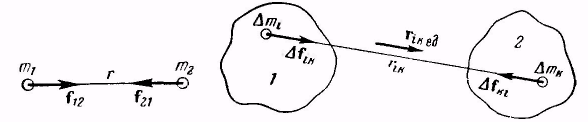
рис. 9.1

вдоль прямой, проходящей через взаимодействующие тела (рис. 9.1). Формула (9.1) дает численное значе­ние равных по величине сил f₁₂ и f₂₁.

Тела, о которых идет речь в соотношении (9.1), представляют собой, очевидно, материальные точки. Для определения силы взаимодействия тел, которые не мо­гут рассматриваться как материальные точки, их нуж­но разбить на элементарные массы Am, т. е. небольшие объемы, каждый из которых можно было бы принять за материальную точку (рис. 9.1). Согласно (9.1) i-я элементарная масса тела притягивается к k-й элемен­тарной массе тела 2 с силой

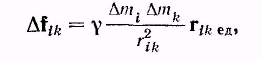(9.2)

Просуммировав (9.2) по всем значениям k, получим результирующую всех сил, действующих со стороны тела 2 на принадлежащую телу 1 элементарную массу m_i: 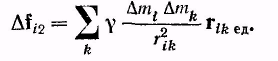(9.3)

Наконец, просуммировав (9.3) по всем значениям индекса i, т. е. сложив силы, приложенные ко всем эле­ментарным массам первого тела, получим силу, с кото­рой тело 2 действует на тело 1: (9.4)

Суммирование производится по всем значениям индек­сов i и k. Следовательно, если тело 1 разбить на n₁, а тело 2 — на n₂ элементарных масс, то сумма (9.4) будет содержать N_{N₂ слагаемых.

По третьему закону Ньютона тело 1 действует на тело 2 с силой f₂₁, которая равна —f₁₂.

Практически суммирование (9.4) сводится к инте­грированию и является, вообще говоря, очень сложной математической задачей. Если взаимодействующие тела представляют собой однородные шары, то вычисление согласно (9.4) приводит к следующему результату:

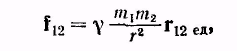(9.5)

Таким образом, шары взаимодействуют, как материальные точки, имеющие массы, равные массам шаров, и поме­щенные в их центрах.

Если одно-из тел представляет собой шар очень боль­шого радиуса R (например, земной шар), а второе тело, не будучи шаром, имеет размеры, гораздо меньшие К, и находится вблизи поверхности шара, то их взаимодей­ствие описывается формулой (9.5), где вместо г нужно взять радиус шара (расстоянием от второго тела до по­верхности шара, а также размерами второго тела мож­но пренебречь по сравнению с К).

Если пользоваться для измерения величин, входящих в (9.1), ранее установленными единицами, то гравитационнай постоянная  оказывается размерной величиной, числен­ное значение которой установлено опыт­ным путем. Размерность её в соответствии с (9.1) равна

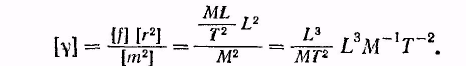
Численное значение  было определено путем изме­рения силы, с которой притягиваются друг к другу тела известной массы. При таких измерениях возникают боль­шие трудности, так как для тел, массы которых могут быть непосредственно измерены, сила притяжения ока­зывается крайне малой. Так, например, два тела с мас­сой 100 кг каждое, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой порядка 10^-6 Н.

Первой успешной попыткой определения  были из­мерения, осуществленные

К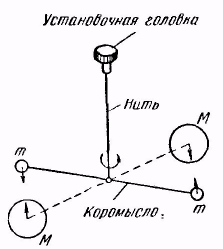 авендишем (1798 г.) кото­рый применил для измерения сил весьма чувствительный

рис. 9.2

метод крутильных весов (рис. 9.2). Два свинцовых шара т (с массой 729 г каждый), прикрепленных к кон­цам легкого коромысла, помещались вблизи симметрич­но расположенных шаров М (с массой по 158 кг). Ко­ромысло подвешивалось на упругой нити, по закручива­нию которой можно было измерять силу притяжения

шаров друг к другу. Верхний ко­нец нити был закреплен в уста­новочной головке, поворотом ко­торой можно было менять рас­стояние между шарами т и М. Наиболее точным из определенных разными способами считает­ся значение

Если в (9.5) подставить m₁ т₂ и r, равные единице, то си­ла оказывается численно рав­ной - Таким образом, два шара с массой 1 кг каждый, центры которых отстоят друг от друга на 1 м, притягиваются взаимно с силой, равной 6,670 • 10^-11 Н.

При изучении движения тел относительно земной поверхности нужно иметь в виду, что система отсчета, связанная с Землей, не инерциальна. Ускорение, соответ­ствующее движению по орбите, гораздо меньше, чем ус­корение, связанное с суточным вращением Земли. Поэто­му можно считать, что система отсчета, связанная с Землей, вращается относительно инерциальных систем с постоянной угловой скоростью . Следовательно, рассматривая движение тел относитель­но Земли, нужно вводить центробежную силу инерции

где т — масса тела, r—расстояние тела от земной оси (рис. 9.3).

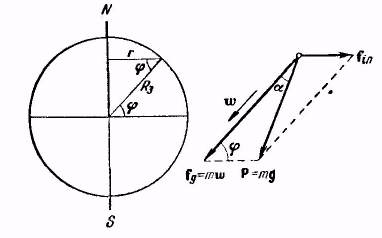
рис.9.3

Ограничиваясь случаями, когда высота тел над по­верхностью Земли невелика, можно положить r равным R_Зсоs. Тогда

(9.6)

Наблюдаемое относительно Земли ускорение свобод­ного падения тел g будет обусловлено действием двух сил: f_g, с которой тело притягивается Землей, и f_in. Ре­зультирующая этих двух сил есть сила тяжести. Поскольку сила Р сооб­щает телу с массой т ускорение g, справедливо сле­дующее соотношение:

Отличие силы тяжести Р от силы притяжения к Зем­ле f<r невелико, так как центробежная сила инерции значительно меньше, чем f_g.(примерно в 300 раз).

Угол  между направлениями f_g и Р можно оценить, воспользовавшись теоремой синусов:

(9.7)

Синус малого угла можно приближенно заменить значе­нием самого угла

Таким образом, в зависимости от широты  угол  колеблется в пределах от нуля (на экваторе и на полюсах) до 0,0018 рад или 6' (на ши­роте 45°).

Направление Р совпадает с направлением нити, натянутой грузом, которое называется направлением отвеса. Сила f_g направлена к центру Земли. Следователь-но, нить отвеса направлена к центру Земли только на полюсах и на экваторе, отклоняясь на промежуточных широтах на угол, определяемый выражением (9.7).

Разность f_g—Р равна нулю на полюсах и достигает максимума, равного 0,3% силы f_g, на экваторе. Из-за сплюснутости земного шара у полюсов сила инерции сама по себе несколько варьирует с широтой, будучи на экваторе примерно на 0,2% меньше, чем у полюсов. В итоге уско­рение свободного падения g меняется с широтой в пре­делах от 9,780 м/сек² на экваторе до 9,832 м/сек² на по­люсах. Значение g = 9,80665 м/сек² принято в качестве нормального (стандартного) значения.