Неинерциальные системы отсчета.

Силы инерции при ускоренном произвольном движении системы отсчета. Центробежная сила. Сила Кориолиса. Вес тела.

Общий случай движения тела в неинерциальной сис­теме отсчета. Возьмем две системы отсчета К и К' (рис. 78), из которых К инерциальна, а К' неинерциальна.

(8.1)

Скорость точки т по отношению к системе К по определению равна

рис. 8. 1

скорость же по отношению к системе К есть

где через d'r' - приращение радиуса-вектора г' по отношению к системе К..

Согласно (8.1) приращение радиуса-вектора r в К-системе

(8.2)

где (см. лекцию по кинематике)

(8.3)

Тогда:

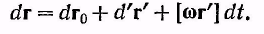(8.4)

Разделив это выражение на dt

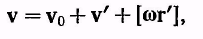(8.5)

Приращение вектора v,

(8.6)

Заменим в этой формуле dr' его значением (8.3), а dv' — аналогичным выражением:

(8.7)

dv' - приращение вектора v', наблю­даемое в системе К, a dv — приращение v', наблюдаемое в системе К. Произведя замену, придем к выра­жению:

Или

Разделим найденное выражение на dt:

Или

(8.8)

где а₀ — ускорение начала координат системы К' («по­ступательное» ускорение системы К').

Умножив вектор a_in=а-ана m и изменив знак на обратный, получим силу инер­ции. Согласно (8.8)

Следовательно,

(8.9)

Формула (8.9) содержит все виды сил инерции. Так, если система К движется относительно системы К только поступательно, без вращения, сила инерции равна

f_in = —mа₀. При наличии вра­щения появляются дополнительно кориолисова сила

(8.9.а) и центробежная сила инерции , которую можно представить в виде (8.9.б).

Кориолисова сила возникает только в случае, когда тело изменяет свое положение по отно шению к вращающейся системе отсчета (при v' = 0 выражение для кориолисовой силы обращается в нуль) Сила Кориолиса всегда лежит в плоскости, перпендикулярной к оси вращения.

Относительно всех инерциальных систем тело обладает одинаковым ускорением а. Поскольку любая НеИСО движется относительно ИСО с некоторым ускорением, ускоре­ние тела в НеИСО a' будет отлично от а. Обозначим разность ускорений тела в а_in:

(8.10)

Если НеИСО движется относитель­но инерциальной поступательно, то а совпадает с уско­рением неинерциалыюй системы отсчета. При враща­тельном движении различные точки неинерциальной системы имеют неодинаковое ускорение.

Пусть результирующая всех сил, обусловленных дей­ствием на данное тело со стороны других тел, равна f, Тогда согласно второму закону Ньютона

Ускорение же относительно НеИСО можно в соответствии с (8.10) представить в виде

Таким образом, даже если результирующая всех сил, приложенных к телу, будет равна нулю, тело будет дви­гаться по отношению к неинерциалыюй системе отсчета с ускорением —а_in, т. е. так, как если бы на него действо­вала сила, равная —та_in.

Следовательно, при описании движения в НеИСО можно пользоваться уравне­ниями динамики, справедливыми только для инерциальных систем, если наряду с силами, обусловленными воздействием тел друг на друга, учитывать так назы­ваемые силы инерции f_in, которые следует полагать равными произведению массы тела на взятую с обрат­ным знаком разность его ускорений по отношению к ИСО и НеИСО:

Тогда уравнение второго закона Ньютона будет иметь вид

Пример

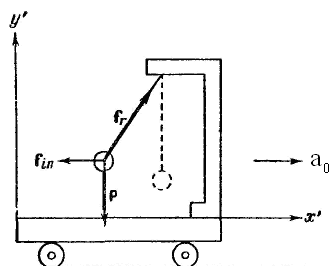
рис. 8.2

Введение сил инерции дает возможность описывать движение тел в любых системах отсчета с помощью одних и тех же уравнений движения.

Силы инерции обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления. В этом смысле их можно назвать фиктивными силами.

Введение в рассмотрение сил инерции не является принципиально необходимым. В принципе любое движение можно всегда рассмотреть по отношению к инерциальной системе отсчета. Однако практически часто представляет интерес как раз движение тел по отноше­нию к неинерциальным системам отсчета, например по отношению к земной поверхности. Использование сил инерции дает возможность решить соответствующую задачу непосредственно по отношению к такой системе отсчета, что часто оказывается значительно проще, чем рассмотрение движения в инерциальной системе.