Геометрический смысл дифференциального уравнения первого порядка
Рассмотрим
дифференциальное уравнение первого
порядка
Возьмём
точку
;
имеем
.
Известно
- тангенс угла наклона касательной к
кривой. То естьдифференциальное
уравнение первого порядка определяет
семейство направлений касательных к
искомым кривым в каждой точке области
,
в которой
и
непрерывны.
Тоесть дифференциальному уравнение
на плоскости соответствует поле направлений
к искомым кривым
Метод изоклин
пусть
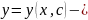линия, на которой
называется изоклиной.
Примеры:
– искомые кривые
5.3. Уравнение Клеро.
Продифференцировав
по x:
Найдём
огибающую семейства
5.4. Уравнение Лагранжа.
Полагая в (2) x(p) – неизвестная функция, p-аргумент имеет уравнение (2) – линейное уравнение.
Решая
его, получим
получим
решение уравнения 1 в параметрической
форме.
6. Дифференциальные уравнения второго порядка. Понижение порядка
Определение
1:Дифференциальным уравнением второго
порядка называется уравнение вида
Определение 2: Начальная задача (Задача Каши).
Задаются начальные условия для уравнения (1)
Требуется
найти частное решение уравнения (1)
Геометрически:
Определение
3:
Определение 4:
Понижение
порядка
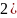
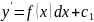
Положим
7. Линейные однородные уравнения второго порядка.
Теоремы 1 и 2.
Определение:
Линейным однородным уравнением второго
порядка называется уравнение вида
Теорема1.
Теорема 2.
Замечание.
Введём
определение: т.е. обозначим
8. Линейная зависимость и независимость решений линейного однородного уравнения второго порядка. Определитель Вронского и его применения.
Определение
1:
Определение
2:
W(x)
Следствие. Формула (4) называется формулой Лиувилля.
Теорема 3.
9.Теорема об общем решение линейного однородного уравнения.
Пусть
p(x)
и q(x)
непрерывна в (a,b).
заданные
.
можно
найти
(1)
Действительно, рассматриваем
систему линейных уравнений (1)
относительно
и
(2)
Опр-ль этой системы
=W(
Замечание.
Пусть
(x)-
частное решение уравнения
(1)
Можно
найти 2-ое частное решение уравнения
(1)
(x)
так, что
-
будет общее решение.
1-й
метод: ищем 2-ое
решение в виде
-U,
где U-
новая неизвестная функция
=>
2-ой метод: Формула Лиувилля:
(x)
известно
10.Линейные однородные уравнения с постоянными коэффициентами.
Рассмотрим 3 случая корней характеристического уравнения:
То
есть можно принять
3)y”+6y’+9y=0
