Лекция № 1 Элементы математической логики
Эта наука оперирует над высказыванием. Под высказыванием понимается повествовательное предложение, подтверждающее тот или иной факт. В алгебре высказываний само содержание высказываний не принимается во внимание. Важным является лишь тот факт, истинное это высказывание или ложное. Высказывания обозначают большими латинскими буквами:
A “ИСТИНА” 1
B “ЛОЖЬ” 0
В обычной речи для образования сложных составных высказываний применяются союзы «и», «или». Кроме того любое высказывание может быть преобразовано в другое высказывание, имеющее противоположный смысл, используя частицу отрицания «не».
Значение истинности составных высказываний зависит от того какой истинностный смысл имеет исходное высказывание.
Операции над высказываниями
Над высказываниями могут быть выполнены следующие логические операции:
1. Отрицание – унарная операция. Для обозначения этой операции применяется значок А и эта операция соответствует применением отрицания «не» к высказыванию. Условие истинности этой операции заключается в том, что отрицание высказывания «А» будет истинным, если само высказывание «А» ложное. А=1, если А=0.
2. Конъюнкция – бинарная операция, то есть выполняется над двумя высказываниями и соответствует применению высказываниям союза «и». Получаемое при помощи союза «и» составное высказывание, имеет истинный логический смысл только в том случае, если оба исходных высказываний одновременно имеют истинный смысл. Обозначается &.
А & В = 1, если А=1 и В=1 одновременно.
3. Дизъюнкция - бинарная операция, соответствует применение союза «или» (v) и составное высказывание имеет истинный смысл в любом случае, если хотя бы одно из исходных высказываний является истинным.
A v B = 1, если А=1 или В=1
4. Эквивалентность (~) – бинарная операция и эта операция имеет истинный смысл тогда, когда оба высказывания имеют одинаковый логический смысл.
А ~ В = 1, если А=1 и В=1
А=0
и В=0
5. Неравнозначность ( ). Истинный смысл этой операции заключается в том, что логические высказывания имеют противоположный смысл.
А В = 1, если А=1 и В=0
А=0 и В=1.
Свободная таблица значений логических операций
А |
В |
А |
В |
А & В |
A v B |
А ~ В |
А В |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Логические операции выполняются над операндами, значение которых детерминировано, то есть заранее определено. В реальной жизни мы не знаем заранее какой логический смысл будет иметь при выполнении того или иного опыта тот или иной операнд. Таким образом, исходные логические высказывания становятся логическими переменными. Поскольку эти логические переменные могут принимать всего лишь 2 значения «0» и «1», то областью определения этих логических переменных является множество их значений.
Х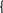
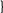i=
0; 1 .
Р езультатом логической операции над этими переменными тоже может быть, либо логический ноль, либо логическая единица. Поэтому логическая операция трансформируется в логические функции, имеющие то же название, что и логическая операция.
Fi= 0, 1 .