Основні властивості інтегрального перетворення Лапласа.
1.
Лінійність
зображення 
.
2.
Теорема
подібності 
.
3.
Диференціювання
оригіналу
;
.
4.
Диференціювання
зображення
.
5.
Інтегрування
оригіналу
6.
Інтегрування
зображення 
.
7.
Теорема
спізнення 
.
8.
Теорема
зміщення 
9.
Теорема
множення (теорема Бореля)
.
Зображення Лапласа деяких функцій
Перетворення
Лапласа застосовується для функцій,
які при від’ємному значенні аргумента
дорівнюють нулю. Такі функції можуть
бути записані у вигляді
,
де
– функція Хевісайда, а
– деяка функція. У подальшому будемо
у більшості випадків випускати множник
,
маючи на увазі його наявність.
Наведемо зображення Лапласа функцій, які найчастіше зустрічаються при розв’язуванні нескладних задач.
; 
;
; 
;
; 
;
; 
.
Існують спеціальні таблиці зображень елементарних та спеціальних функцій, які наведені у посібниках з інтегральних перетворень та довідниках .
Якщо
функція
є кусочно неперервною, наприклад, має
вигляд
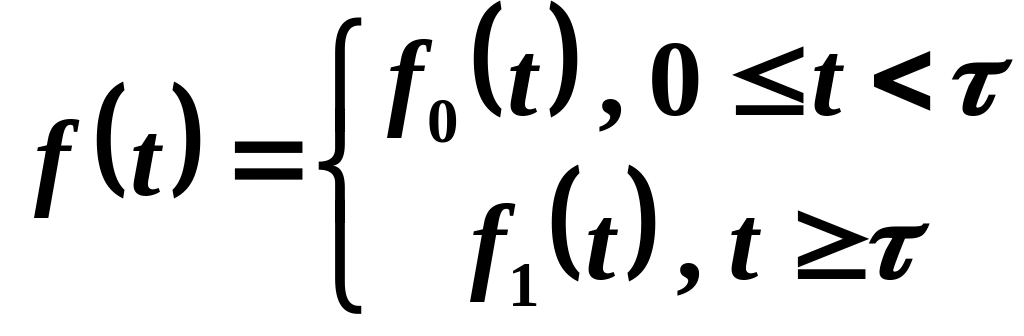, її можна записати за допомогою функції
Хевісайда у вигляді
,
або
.
Тоді відповідне зображення має вигляд
.
Зокрема, зображенням функції
буде
.
Визначення оригіналу за відомим зображенням
Якщо
відомо, що задана функція
в області
є зображенням кусочно гладкої функції
,
степінь зростання якої не перевищує
,
то
,
.
Наведена рівність називається формулою Мелліна.
Якщо функція є правильним раціональним дробом, то її оригінал можна побудувати за формулою
.
Зокрема,
якщо всі полюси функції
є
простими, то
,
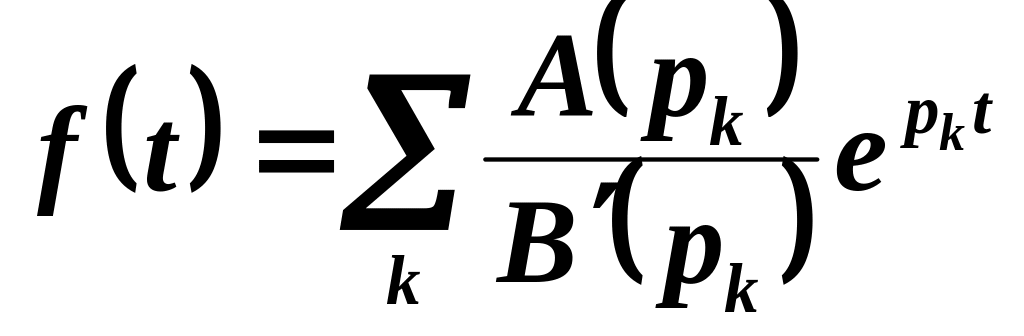причому, якщо серед полюсів є комплексно спряжені, то формула набуває вигляду
,
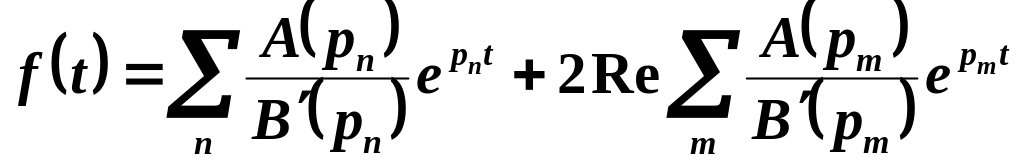де
– дійсні полюси, а
– комплексні полюси з додатною уявною
частиною.
Дуже важливим з практичної точки зору є також відшукування оригіналу методом підбору: записують зображення у вигляді суми функцій, оригінали яких відомі, та представляють шуканий оригінал як суму цих оригіналів.