44.Ізотерми Ван-дер-Вальса.Порівняння зексперементальними ізотермами

З рівняння Менделєєва–Клапейрона виходить, що при Т = const і m = const залишається постійним добуток PV = const, тобто це ізотермічний закон Бойля-Маріотта, звідки P=const/V . З рівняння Ван-дер-Ваальса випливає більш складна залежність P = f(V) при постійній температурі: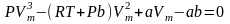 . Отримане рівняння є алгебраїчним рівнянням третього степеня відносно молярного об’єму. Існує критична температура Т_к: при T>Т_к ізотерми реального газу майже не відрізняються від ізотерм ідеального газу, при T<Т_к є область станів, де ізотерма має хвилеподібну ділянку і кожному значенню тиску відповідають три точки ізотерми. При підвищенні температури ці точки зближуються і при T=Т_к зливаються в одну точку К, яка є точкою перегину ізотерми при T=Т_к. При підвищенні температури до критичної Т = Т_к отримуємо критичну ізотерму без хвилеподібних ділянок. При цій температурі зникає різниця між газоподібним і рідким станом речовини. Відповідні тиск Р_к і молярний об’єм V_mк також називаються критичними, а стан з критичними параметрами речовини Р_к, V_mк, Т_к називається критичним станом. Критичні параметри Р_к, V_mк, Т_к можна знайти з рівняння Ван-дер-Ваальса через сталі a i b:

, , .

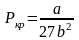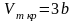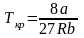Пара відрізняється від інших газоподібних станів тим, що при ізотермічному стисканні відбувається процес зрідження. А газ, який знаходиться при температурі вищій за критичну T>Т_к, не може бути перетворений стисканням на рідину.

48.Внутрішня енергія реального газу

Внутрішня енергія реального газу U складається з кінетичної енергії теплового руху його молекул (визначає внутрішню енергію ідеального газу, що дорівнює U_к = C_VT для одного моля) і потенціальної енергії міжмолекулярної взаємодіїU_n . Потенціальна енергія реального газу зумовлена лише силами притягання між молекулами, які приводять до виникнення внутрішнього тиску на газ 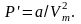Робота, яка витрачається для подолання сил притягання, що діють між молекулами газу, іде на збільшення потенціальної енергії системи, тобт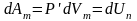о або 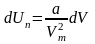. Звідси знаходимо потенціальну енергію одного моля реального газу: 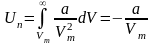. Знак "-" означає, що молекулярні сили, які створюють внутрішній тиск, є силами притягання. Тоді повна внутрішня енергія одного моля реального газу дорівнює .

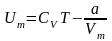Вона зростає зі збільшенням температури й об’єму газу.Якщо газ розширюється без теплообміну з навколишнім середовищем і не виконує роботу, то на підставі першого закону термодинаміки одержимо, що 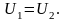Отже, при адіабатичному розширенні без здійснення зовнішньої роботи внутрішня енергія газу не змінюється. Для ідеального газу це означає, що при адіабатному розширенні у вакуум (тобто без виконання роботи) його температура не змінюється Т₁ = Т₂. 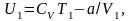Для реального газу, з огляду на те, що для одного моля газу 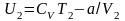, одержуємо 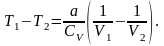Оскільки V₂ > V₁ , то T₁ >T₂, тобто реальний газ при адіабатному розширенні у вакуум охолоджується.

53.Теплопровідність твердих тіл

Знайдемо внутрішню енергію одного моля твердого тіла, яке має атомну кристалічну решітку, у вузлах якої знаходяться атоми, що коливаються відносно свого рівноважного положення. Внутрішня енергія дорівнює сумі енергій частинок, що утворюють кристалічну решітку. Частинки мають як кінетичну, так і потенціальну енергію, які в середньому дорівнюють одна одній. На одну ступінь вільності молекули, згідно із законом Больцмана (див. п.2.2.1), припадає у середньому кінетична енергія, що дорівнює kT/2. Таким чином, на одну коливальну ступінь вільності припадає енергія kT. Оскільки частинка може коливатися відносно положення своєї рівноваги у будь-якому напрямку, звідси випливає, що вона має три ступені вільності (і = 3). Тому значення повної середньої енергії атома _о = 3kT.

З урахуванням вищевикладеного внутрішня енергія одного моля атомарного кристала дорівнює U_m = _оN_A = 3kTN_A = 3RT. З іншого боку, оскільки об’єм твердого тіла величина стала, U_m = С_V T.

Звідси: 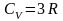, тобто молярна теплоємність усіх хімічно простих кристалічних тіл однакова. Ця залежність називається законом Дюлонга і Пті. Вона була експериментально встановлена цими вченими 1819 р.

Для хімічно складних тіл молярна теплоємність 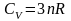(де п – число атомів у молекулі).

Експерименти показують, що закон Дюлонга і Пті виконується тільки за досить високої температури (Т300 К), а навіть за кімнатної температури має наближений характер. Зі зниженням температури теплоємність усіх твердих кристалічних тіл зменшується С_V T ³ і в міру наближення до абсолютного нуля прямує до нуля. Поведінка теплоємності за низьких температур була пояснена Ейнштейном і Дебаєм, виходячи з квантової теорії.