Раздел 4

МОДЕЛИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

4.1. Общие принципы динамического программирования

Рассмотрим экономическую систему S, состояния которой фиксируются в дискретные моменты времени (или какого–то другого аргумента). Под состоянием системы S понимают вектор, т.е. совокупность параметров, характеризующих функционирование системы (например, объем выпускаемой продукции, качество продукции, доля продукции на экспорт, потребление электроэнергии и др.) В дальнейшем – множество всех возможных состояний в момент – конкретное состояние из . Если система S находится в состоянии x_k, то под действием определенного управления из множества управлений она может перейти в некоторое состояние . Под управлениями можно понимать: выделение определенной суммы какому-либо подразделению; выбор технологии производства из нескольких возможных; административное управленческое решение; выбор маршрута движения и т.д. Следует отметить, что конкретные управления и множество управлений зависит, вообще говоря, и от состояний системы, т.е. Для простоты обозначений этот факт пока опускается.

Предполагается, что в начальный момент система S находилась в конкретном состоянии и затем последовательно, под действием управлений, переходила в некоторые состояния . В результате перехода от к произведена прибыль (или совершены затраты), которые обозначим через ( – целевая функция). Обозначим для краткости: – последовательность управлений, переводящих S из состояния в некоторое состояние – совокупность всех возможных управлений вида Тогда функция F запишется в виде

Задача состоит в следующем: выбирая на каждом этапе подходящие управления, добиться того, чтобы функция F приняла экстремальное значение.

Для решения этой задачи введем дополнительные предположения:

1. (4.1.1)

т.е. не зависит от того, как система S пришла в состояние .

2. (4.1.2)

т.е. F – аддитивна, где – прибыли (затраты) при переходе S из состояния в .

Тогда задачу динамического программирования можно записать в виде:

(4.1.3)

где экстремум берется по всем . В названии динамическое программирование слово программирование означает принятие решений (планирование), а слово динамическое указывает на существенную роль времени и порядка выполнения операций.

Принцип инвариантного погружения. Функция Беллмана

Вместо задачи (4.1.3) будем рассматривать множество задач, состоящих в следующем: в качестве начального возьмем произвольный момент ; начальным состоянием будем считать произвольное состояние Получим семейство задач:

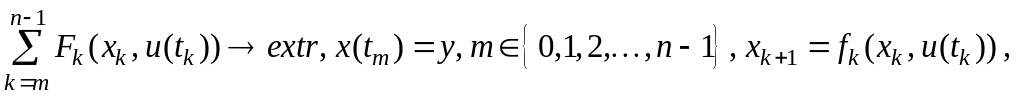(4.1.4)

где экстремум берется по всем управлениям , переводящим S из состояния в некоторое состояние . Переход от задачи (4.1.3) к семейству задач (4.1.4) называют принципом инвариантного погружения. Ниже будет показано, что этот переход позволяет свести решение задачи (4.1.3) к множеству более простых задач. Для этого введем следующее определение.

Функция

(4.1.5)

где экстремум берется по всем допустимым управлениям задачи (4.1.4), называется функцией Беллмана для задачи (4.1.4). Управление, при котором достигается экстремум функции при конкретных m и y, называется оптимальным управлением. Его можно обозначить символом