1

Понятие математической модели.

Моделирование конкретной физической задачи обычно включает в себя несколько этапов:

1. построение физической модели явления;

2. формулировка соответствующих математических уравнений, начальных и граничных условий;

3. исследование возможности аналитического решения в рамках упрощенной модели, качественное исследование влияния параметров задачи на ее решение;

4. выбор численного метода решения исходной математической задачи;

5. анализ полученного решения, сравнение с имеющимися в наличии экспериментальными данными и прогнозирование возможных экспериментальных результатов.

модель является динамической, т.е. описывает изменение состояния системы с течением времени. Если состояние системы с течением времени не изменяется, такие модели называются статическими.

После того как математическая модель сформулирована, на ее основе ставят и решают математическую задачу. Для этого все величины, включенные в математическую модель, условно разбивают на 3 группы:

1. исходные (входные) данные х;

2. параметры модели а;

3. искомое решение (выходные данные) у.

В динамических моделях все или некоторые из этих величин зависят от времени t.

Основными типами рассматриваемых задач являются следующие:

1. прямые задачи, когда по данному значению входных данных х при фиксированных значениях параметров а требуется найти решение у;

2. обратные задачи, когда по данным значениям у при фиксированных значениях параметров а нужно определить входные данные х (обратные задачи, как правило, сложнее прямых);

3. задачи идентификации, когда среди множества всевозможных моделей нужно выбрать ту, которая наилучшим образом описывает рассматриваемое явление.

Приведем пример простейшей математической модели.

Пусть исследуется движение тела, брошенного со скоростью v₀ под углом  к горизонту.

Введем следующие предположения, существенно упрощающие построение модели исследуемого явления:

1. сопротивлением воздуха можно пренебречь,

2. Землю можно считать плоской,

3. Ускорение свободного падения g постоянно.

y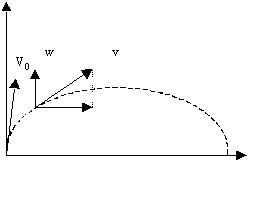

Пусть v_l(t) и v_h(t) – горизонтальная и вертикальная составляющие скорости v(t) в момент времени t, соответственно.

2

Устойчивость.

В процессе решения задач математического моделирования возникают три основных проблемы:

1. адекватность дискретной модели исходной математической задаче;

2. сходимость численного решения к точному решению;

3. устойчивость выбранного метода решения.

Вопрос устойчивости связан со степенью нарастания в ходе расчета ошибок округления и других ошибок, связанных с проводимыми вычислениями, что во многих случаях может привести к полному искажению результата.

Пример.

Заменим производную в уравнении (42) ее симметричной разностной аппроксимацией. В результате получится рекуррентная формула

(49)

Будем этим методом искать решение задачи

(50)

точное решение которой равно

Использовав разложение искомой функции в ряд Тейлора с точностью до квадратичных членов, получим

Расчет по формуле (49) показывает, что при малых х численное решение в пределах погрешности хорошо согласуется с точным. Затем вблизи х3.5 в численном решении развиваются осцилляции, размах которых нарастает, в конечном счете полностью подавляя ожидаемый экспоненциальный спад для y(x).

Данное поведение является признаком неустойчивости применяемого алгоритма.

Чтобы понять причину этой неустойчивости, перепишем уравнение (49) в виде

y_n+1 = y_n-1 - 2y_n . (51)

Будем искать решение уравнения (51) в виде , где A,r - некоторые константы. Подставляя в (51), получаем уравнение для r:

Двумя корнями полученного уравнения являются значения

Отрицательному корню соответствует решение

 ,

изменяющее знак при каждом переходе к следующему узлу сетки. Из-за ошибок округления некоторая часть этого решения будет постоянно вноситься в общее решение исходного уравнения, и в конце концов побочное решение станет доминировать.

Особое внимание на проблему устойчивости следует обратить в задачах, где ожидаются строго убывающие решения.

3