6.2Параметрические ёмкостные элементы
Параметрическая ёмкость достаточно просто реализуется на специальном полупроводниковом диоде, который называется варикап. Параметрическая ёмкость, используемая в высокочастотном диапазоне, иногда называется варактором. Если к полупроводниковому диоду приложить напряжение обратной полярности, то величина заряда в области запирающего слоя зависит от приложенного напряжения. Полученная зависимость называется вольт-кулонной характеристикой параметрического конденсатора (ВКХ). Если изменять приложенное напряжение, то ток через диод (ток смещения) будет равен:
Сдиф(u) – диффузионная ёмкость конденсатора, она зависит от приложенного напряжения следующим образом:
С (0) – ёмкость
φк – контактная разность потенциалов, которая зависит от кристалла, примеси и других факторов.
Современные варикапы работают на частотах до 10 ГГц, в миллиметровом диапазоне волн.
Рассмотрим зависимость между ёмкостью конденсатора и запасённой в нём энергии. Пусть имеется плоский конденсатор, расстояние между пластинами равно – х, площадь пластин S, и конденсатор заряжен до напряжения u. Тогда ёмкость конденсатора будет равняться:
Заряд:
Энергия, запасённая в конденсаторе будет равняться:
Рассмотрим изменение энергии при q = const:
Таким образом, если заряд остаётся постоянным, то запас энергии в конденсаторе возрастает при уменьшении ёмкости, и уменьшается при её увеличении, т. е. изменение энергии, запасённой в конденсаторе, происходит за счет работы, совершаемой при перемещении обкладок.
Для увеличения энергии, запасённой в конденсаторе, необходимо за счет внешних сил уменьшить ёмкость заряженного конденсатора. Если ёмкость изменять периодически, то средняя энергия, запасённая в конденсаторе, изменяться не будет, т. к. на интервалах уменьшения ёмкости энергия в конденсаторе возрастает, а на интервалах увеличения ёмкости уменьшается на ту же величину.
Однако энергию, запасённую в конденсаторе, можно изменять, если напряжение на конденсаторе изменяет знак, т. е. проходит через ноль.
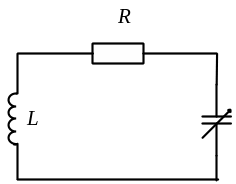
Рассмотрим высокодобротный колебательный контур, в котором ёмкость изменяется во времени С(t). Будем считать, что напряжение на ёмкости изменяется по гармоническому закону, это возможно, если в контуре возбуждены собственные колебания, частота которых вычисляется по следующей формуле:
где С0 – ёмкость при нулевом приложенном напряжении.
Предположим, что ёмкость изменяется скачком, причём в моменты прохождения напряжения на ёмкости через нулевое значение ёмкости увеличивается, а в моменты, когда напряжение достигает максимального значения, величина ёмкости уменьшается:
В моменты, когда
= 0 (момент увеличения ёмкости), энергия
запасённая в конденсаторе равна нулю,
т. к.
,
поэтому при увеличении ёмкости её
энергия не изменяется (
следовательно
).
В моменты уменьшения ёмкости энергия, запасённая в контуре будет равняться:
,
поэтому
На периоде ёмкость
уменьшается в два раза, поэтому на
периоде в ёмкость будет внесена энергия
– энергия накачки.
Накачка энергии в контуре будет происходить в Ом случае, если в законе изменения ёмкости во времени имеется составляющая с частотой 2с и поддерживаются определённые фазовые соотношения.
Рассмотрим зависимость между напряжением и током в параметрическом конденсаторе. Для этого рассмотрим следующую цепь:
Таким образом, ток кроме колебания с основной частотой с содержит боковые колебания с частотами (с н). Передача мощности от источника к нагрузке при гармонических напряжениях и токах происходят в том случае, когда напряжение и ток имеют одинаковую частоту, а фазовый сдвиг между током и напряжением отличен от 90.
Первая составляющая
тока имеет частоту, совпадающую с
частотой напряжения, но опережает по
фазе на угол
,
поэтому эта составляющая не будет
выделять энергию на конденсаторе.
Третья составляющая тока также не будет выделять энергии на конденсаторе, т. к. частота тока с + н = с.
Вторая составляющая тока может изменять энергию, запасённую в контуре, если её частота будет равна частоте напряжения:
Это возможно при
Определим среднюю мощность, выделяемую на периоде:
Схему замещения параметрического конденсатора можно представить в следующем виде:
Величину вносимого сопротивления определим из условия баланса мощностей, т. е. мощность, выделяемая на вносимом сопротивлении равна:
и она должна равняться мощности на конденсаторе:
Sin, стоящий в знаменателе, можно принимать как положительные так и отрицательные значения, поэтому Rвн может быть положительная и отрицательная. Если Rвн > 0, то параметрическая ёмкость рассеивает энергию, поступающую из внешней цепи. Если Rвн < 0, то параметрическая ёмкость отдаёт энергию во внешнюю цепь, т. е. ведет себя подобно генератору.
Параметрические ёмкости применяются для построения параметрических усилителей, которые нашли широкое применение в СВЧ – диапазоне и используются во входных каскадах радиоприёмных устройств.
Достоинством этих усилителей является низкий уровень собственных шумов.