39.1Цепь синусоидального тока с емкостью.

     Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

.

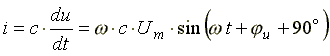      Из анализа выражений следует, что ток опережает напряжение по фазе на 90^o.

      Выражение в комплексной форме записи имеет вид:

,    

       где 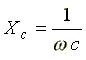- емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

        Если комплексное сопротивление индуктивности положительно         , то комплексное сопротивление емкости отрицательно         .

       На рис. а изображена векторная диаграмма цепи с емкостью.        Вектор тока опережает вектор напряжения на 90^o.

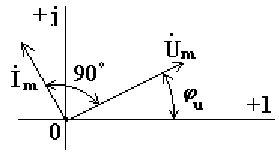
Рис. а

39.2.Энергетический процесс.

Хз что это за фигня

39.3.Мгновенная, активная и реактивная мощности.

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Активная мощность – среднее за период значение мгновенной мощности.

где cosφ –коэффициент мощности, φ – угол сдвига фаз между напряжением и током. P=[Вт] Для резистора P=UIcos0=UI=I^2R=(U^2)/R

На индуктивном элементе: P=UIcos(π/2)

На емкостном элементе: P=UIcos(-π/2)

Реактивная мощность – характеризует интенсивность обменного процесса в цепи переменного тока. Q=UIsinφ=[ВАр]

Полная мощность: S=[ВА]

40.Последовательное соединение резистора и конденсатора (конденсатор с потерями). Временная и векторная диаграммы. Закон Ома для действующих и амплитудных значений тока и напряжения.

Последовательное соединение резистора и конденсатора (конденсатор с потерями).       Конденсатор (ёмкость) –элемент, способный накапливать электромагнитную энергию в собственном электрическом поле, образуемом обкладками конденсатора. Обозначается – С. Напряжение и ток на его контактах связано зависимостью:

      Величина ёмкости измеряется в фарадах (Ф). 1 фарада – это величина такой ёмкости, на которой имеет место падение напряжения 1 вольт при наличии заряда в ёмкости 1 кулон.        1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: - пикофарад – 10^-12; нанофарад – 10^-9; микрофарад – 10^-6.

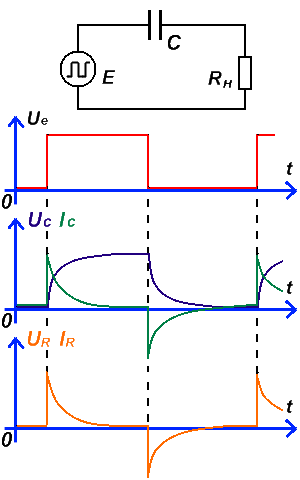
      Процессы, происходящие в конденсаторе на временном графике при подключении конденсатора к источнику прямоугольного однополярного сигнала, показаны на рисунке.        Из рисунка видно, что в момент подачи прямоугольного импульса источника тока (красный), напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и с изменением времени увеличивается по экспоненте – конденсатор заряжается, а ток конденсатора (зелёный) наоборот сначала максимален, но потом по мере заряда уменьшается по экспоненте. При пропадании импульса, напряжение на выводах конденсатора уменьшается по экспоненте – конденсатор разряжается, а ток, изменивший полярность сначала максимален, и по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от значения ёмкости. Чем больше ёмкость, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Их взаимосвязь описывается законом Ома.

      Фактически, мы рассмотрели «четырёхполюсник» состоящий из конденсатора и резистора, который называют дифференцирующей цепочкой.        Дифференцирующая цепочка применяется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Чтобы, Вам было понятнее, дифференцирующая цепочка и преобразование импульса изображены на следующем рисунке.        Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.

      Кроме функции преобразования прямоугольных импульсов, дифференцирующая цепочка может применяться в качестве фильтра высоких частот (ФВЧ). Конденсатор – инертный элемент. Если к конденсатору с большой ёмкостью приложить переменное напряжение низкой частоты, в силу своей инертности, ёмкость будет не способной пропустить через себя ток, ведь конденсатору сначала надо будет зарядиться, а потом отдавать заряд. Свойство конденсатора сопротивляться переменному электрическому току называют реактивным сопротивлением конденсатора, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается Xcили Zc и измеряется в Омах. Реактивное сопротивление конденсатора связано с собственной ёмкостью и частотой тока выражением:

      Из формулы видно, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами, чем выше частота, тем меньше реактивное сопротивление конденсатора.        Теперь представьте, что дифференцирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает конденсатор. А мы из формулы теперь знаем, что конденсатор легко пропускает высокие частоты – его сопротивление минимально и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.        То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо - АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.        Зная, как рассчитывается делитель напряжения и реактивное сопротивление конденсатора на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр высокой частоты на конденсаторе и резисторе.

      Если в дифференцирующей цепочке поменять местами конденсатор и резистор, то мы получим – интегрирующую цепочку. Все процессы в интегрирующей цепочке происходят точно так же, как и в дифференцирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для интегрирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а конденсатор. Поэтому, на выходе интегрирующей цепи будут не остроконечные дифференцированные импульсы (зелёного цвета), а импульсы напряжения, которое присутствует на выводах конденсатора (фиолетового цвета). Ну а если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке - оранжевого цвета, и частота среза равная значению f1.

      Cледует добавить, частотные фильтры, выполненные на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом позже, когда изучим катушку индуктивности.

Временная и векторная диаграммы.

Евдокимов стр.255-258

Закон Ома для действующих и амплитудных значений тока и напряжения.

Пусть источник тока создает переменное гармоническое напряжение (рисунок)

U(t) = U_osinωt. (1)

Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:

I(t) = U(t)/R = (U_o/R)sinωt = I_osinωt,

где I_o = U_o/R ? амплитудное значение силы тока в цепи. Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины U_o и I_o = U_o/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными. Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность P(t) = U(t)I(t), которая, в отличие от цепей постоянного тока, изменяется с течением времени. С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде

P(t) = U(t)I(t) = I²(t)R = I_o²Rsin²ωt.

Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно. Перепишем формулу для мощности по-другому:

P = UI = U_oI_osin²ωt = (1/2)U_oI_o(1 ? cos2ωt) = U_oI_o/2 ? (U_oI_o/2)cos2ωt.

Первое слагаемое не зависит от времени. Второе слагаемое ? переменная составляющая ? функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рисунок). Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле

P_cp = U_oI_o/2 = I_o²/R.

Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока. Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток. Поскольку для постоянного тока

P_пост =I²R,

то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока

I_д = I_o/?2.

Аналогично можно ввести действующее значение и для напряжения

U_д = U_o/?2.

Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

P = U_дI_д = I_д²R = U_д²/R, I_д = U_д/R.