24. Метод монте карло.

Ме́тод Мо́нте-Ка́рло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики, экономики, оптимизации, теории управления и др.

Геометрический алгоритм Монте-Карло интегрирования

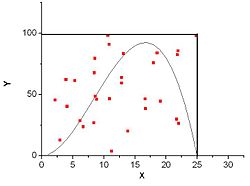
Рисунок 3. Численное интегрирование функции методом Монте-Карло

Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:

ограничим функцию прямоугольником (n-мерным параллелепипедом в случае многих измерений), площадь которого можно легко вычислить;

«набросаем» в этот прямоугольник (параллелепипед) некоторое количество точек ( штук), координаты которых будем выбирать случайным образом;

определим число точек ( штук), которые попадут под график функции;

площадь области, ограниченной функцией и осями координат S, даётся выражением

Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным.

25. Метод статистического моделирования и его сущность. Примеры статистического моделирования.

В методичке №5 стр 4.

26. Для решении каких задач применяют метод статистического моделирования. –

в методичке №5 стр.5 конец.

27. Какие основные этапы включает алгоритм статистического моделирования.

Ответ в методичке №5. Стр 4конец-5начало

28. Что из себя представляет статистический эксперимент стр 4- 3 абзац

29. Понятие последовательности случайных чисел.

Это последовательность элементы которой не зависят друг от друга , но подчиняются определенному закону распределения.

Законы распределения – методичка №4 стр 7к-ц-8нач.

Способы их получения. Ответ в мет.№4 стр 4 к-ц-5нач.

30. назовите основные характеристики случайных величин и поясните как вычисляются.

Характеристики случайных величин:

1) Математическое ожидание.

Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений хi с вероятностями рi , называется сумма:

М ( Х ) = х1 · р1 + х2 · р2 + х3 · р3 + ... + хn· рn .

2)Свойства математического ожидания.

1) М ( с · Х ) = с · М ( Х ) , c R ,

2) М ( Х + Y ) = М ( Х ) + М ( Y ) , Х , Y Е ,

3) М ( Х · Y ) = М ( Х ) · М ( Y ) для независимых случайных величин Х и Y .

3)Дисперсия.

Дисперсией случайной величины Х называется число:

D ( Х ) = М{ [ Х – М ( Х )] 2 }= М ( Х 2 ) – [М ( Х )] 2

4)Свойства дисперсии.

1) D ( с · Х ) = с 2 · D ( Х ) , c R ,

2) D ( Х + Y ) = D ( Х ) + D ( Y ) для независимых случайных величин Х и Y .

5)Среднее квадратичное отклонение.

показатель рассеивания значений случайной величины относительно её математического ожидания. Равно корню квадратному из дисперсии случайной величины.

31. Область применения последовательностей случайных чисел.

Какие вы знаете методы генерации случайных чисел, распределенных по равномерному закону.

Ответ в методичке №4 стр 5-6.

32. Каким образом можно получить случайные числа распределенные по закону отличного от равномерного?

Ответ в методичке № 4, стр 7-конец-8начало.

33

34. Какие основные типы ГСЧ вы знаете?

Ответ в методичке №4, стр4 конец-5 начало.