6.2. Ймовірність станів
Основною
характеристикою марковських ланцюгів
є ймовірності
станів системи на
-му
кроці, тобто ймовірності того, що система
від
-го
до
-го
кроку перебуватиме у стані
.
Визначення
6.4.
Імовірності
називають ймовірностями станів. Для
кожного кроку
події
несумісні й утворюють повну групу подій,
отже,
Визначення
6.5.
Перехідними
ймовірностями
з
-го
в
-й
стан системи для
-го
кроку
називаються ймовірності безпосереднього
переходу системи
у момент часу
зі стану
в стан
.
Визначення
6.6.
Якщо
,
то перехідна ймовірність
називається
ймовірністю затримки системи
в стані
.
Визначення
6.7. Якщо
перехідні ймовірності не залежать від
номеру кроку
,
марковський процес називається однорідним
і перехідні ймовірності позначаються
замість
.
Якщо ж хоч би одна ймовірність змінюється з номером кроку , то марковський ланцюг називається неоднорідний.
Запишемо перехідну ймовірність Марковського ланцюга у вигляді квадратної матриці -го порядку
.
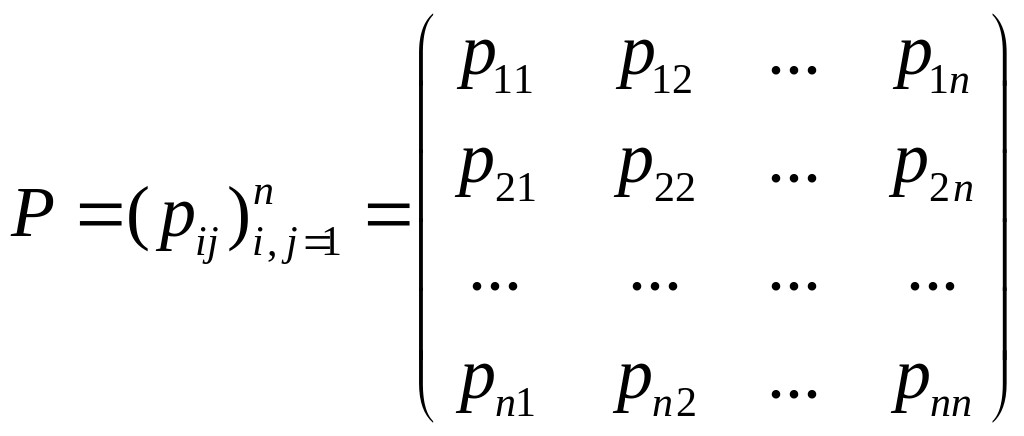Матриця
не залежить від номера
,
її порядок
співпадає з числом станів системи, на
головній діагоналі розташовані
ймовірності затримок.
Перехідні ймовірності інтерпретують як умовні ймовірності
подій
(з
-го
до
-го
кроку система
знаходиться в стані
)
за умови, що мали місце події
.
Враховуючи, що події несумісні й утворюють повну групу подій, матимемо
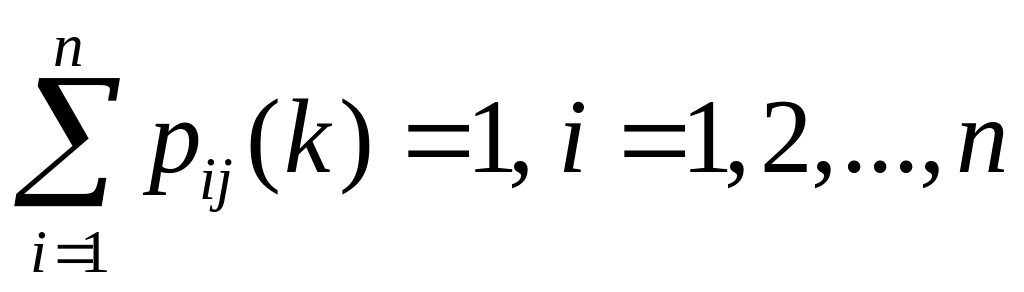
Тобто сума елементів кожного рядка матриці перехідних ймовірностей дорівнює 1.
Визначення 6.8. Матриця, кожен елемент якої невід’ємний, а сума елементів кожного рядка дорівнює одиниці, називається стохастичною.
Таким чином, матриця перехідних ймовірностей є стохастичною.
Визначення 6.9. Якщо у стохастичної матриці сума елементів кожного її стовпця дорівнює одиниці, то вона називається двояко стохастичною.
Приклад 6.1. На рисунку 6.2 зображено розмічений граф (у гілок якого вказані перехідні ймовірності). Відсутність гілок між станами говорять про те, що відповідна перехідна ймовірність дорівнює нулю.
Рисунок 6.2 – Приклад розміченого графа системи
Наприклад,
,
в той час як
.
Перехідні ймовірності, що відповідають гілкам, які починаються зі стану розташовані в -му рядку матриці перехідних ймовірностей, а сума їх, згідно з умовою нормування дорівнює 1. Користуючись цим, розраховують імовірність затримок, а гілки – петлі на графі не вказують
.
Вектор-рядок
ймовірностей станів
в початковий момент часу
,
безпосередньо передуючий першому кроку,
називається вектором початкового
розподілу ймовірностей. Для ймовірностей
в початковий момент часу також справедлива
умова нормування, тобто при
.
Так,
якщо система
в
початковий момент часу
знаходилася в стані
,
то
,
а тоді початковий розподіл ймовірностей
матиме вигляд
.
Якщо відомий початковий розподіл ймовірностей і матриця перехідних ймовірностей, можна обчислити ймовірності стану системи від будь-якого -го до -го кроку. Має місце наступна теорема.
Теорема
6.1.
Для
однорідного марковського ланцюга
вектор-рядок ймовірностей станів від
-го
до
-го
кроку дорівнює добутку вектора-рядка
ймовірностей станів від
-го
до
-го
кроку та матриці перехідних ймовірностей
.
Наслідок. Для однорідного Марковського ланцюга справедлива наступна формула
.
Приклад 6.2. Стани банку характеризуються однією з відсоткових ставок: 2%, 3%, 4%, які встановлені на початку кожного кварталу і фіксовані протягом кварталу. Таким чином, якщо за систему прийняти банк, то вона в кожен момент часу може знаходитися тільки в одному з наступних трьох станів: – відсоткова ставка 2%, – відсоткова ставка 3%, – 4%. Аналіз роботи банку в попередні роки показав, що зміни перехідних ймовірностей з часом настільки незначні, що ними можна знехтувати. Охарактеризувати процес і визначити ймовірності вказаних станів наприкінці року, якщо наприкінці попереднього року відсоткова ставка банку складала 3%, розмічений граф станів банку зображено на рисунку 6.3.
Рисунок 6.3 – Розмічений граф станів
Розв’язання. Оскільки множина станів, в яких може знаходитися система , скінчена (три стани), то випадковий процес, що протікає у системі дискретний.
З певним ступенем похибки можна припустити, що ймовірність перебування в одному зі своїх станів в майбутньому істотно залежить тільки від його стану зараз і не залежить від його станів у минулому. А тому даний випадковий процес можна вважати марковським.
За умовою
банк може переходити зі стану в стан
тільки в наперед визначені моменти
часу:
– початок
-го
кварталу,
.
Отже, випадковий процес в системі
є процесом з дискретним часом. Оскільки
залежність перехідних ймовірностей
від часу можна знехтувати. То даний
процес однорідний марковський ланцюг.
За розміченим графом впишемо значення перехідних ймовірностей:
Тоді за
умовами нормування при
.
Аналогічно
,
отже,
Складемо матрицю перехідних ймовірностей
.
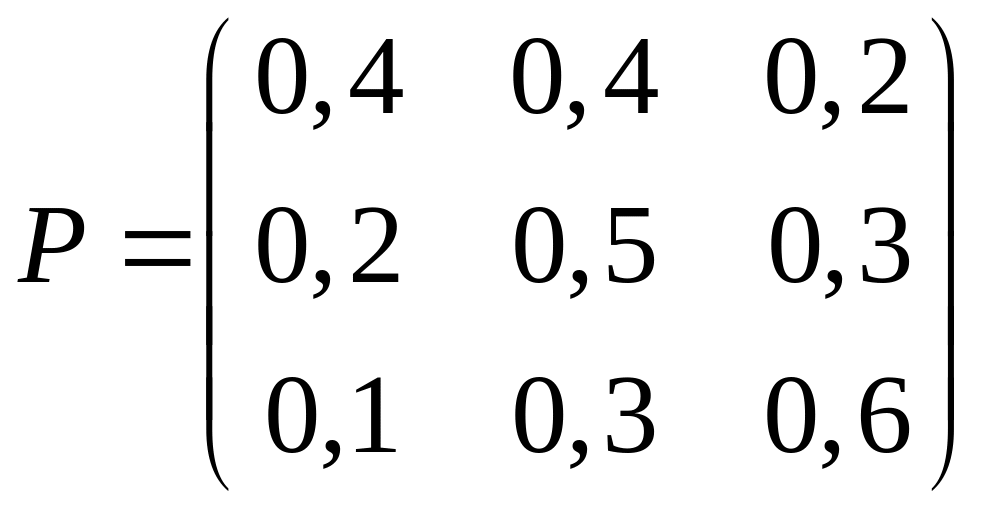Потрібно звернути увагу на те, що сума елементів кожного рядка матриці дорівнює 1.
Оскільки наприкінці попереднього року відсоткова ставка складала 3%, то можна вважати, в початковий момент система знаходиться в стані . Тому початковий розподіл ймовірностей має вигляд
Ймовірність
станів банку наприкінці року, тобто
після чотирьох кварталів, можна знайти
при
та
за формулою:
.
У результаті розрахунку отримаємо
Тобто, наприкінці року ймовірність відсоткових ставок 2%, 3%, 4% дорівнюють відповідно 0,2020, 0,4015, 0,3965. Таким чином найімовірніше відсоткова ставка до кінця року не зміниться і буде складати 3%. Як контроль на правильність обчислень можна використовувати перевірку матриці на стохастичність.
ЛЕКЦІЯ 7 МАРКОВСЬКИЙ НЕОДНОРІДНИЙ ЛАНЦЮГ З ДИСКРЕТНИМ ЧАСОМ