5.2. Приклади процесів у фінансово-економічній галузі, які є марковськими процесами

Приклад 5.1. Побудувати реалізацію випадкового процесу для інтервалу часу з 10.00 до 11.00, що протікає в системі, граф стану якої має вигляд, наведений на рисунку 5.3.

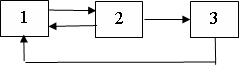
Рисунок 5.3 – Граф станів системи

Розв’язання. Нехай о 10.00 система знаходилася у стані , потім в 10.15 перейшла в стан , в 10.25 – повернулася в , в 10.40 – перейшла в і продовжувала залишатися в ньому.

При побудові реалізації потрібно звернути увагу на те, що система не може за один крок перейти зі стану в стан , оскільки такий перехід заборонений (на графі немає гілки, що дозволяє такий перехід). Для зручності запису припишемо кожному стану свій номер: – 1; – 2; – 3.

На осі часу відкладемо відповідні часові проміжки та отримаємо у результаті ступінчасту розривну функцію (рис. 5.4).

Рисунок 5.4 – Графічна реалізація випадкового процесу

Це графічна форма представлення реалізації. Аналітична форма має наступний вигляд:

Приклад 5.2. Розглянути роботу вікна обслуговування клієнтів у комерційному банку. Побудувати модель роботи вікна. Охарактеризувати процес. Побудувати граф станів роботи системи та реалізацію (графічну, аналітичну).

Розв’язання. Інтерпретувати роботу вікна як систему . Система має два стани:

– вікно вільне;

– вікно зайняте.

Процес, що протікає у системі – випадковий, оскільки прихід відвідувачів у банк у загальному випадку носить випадковий характер. Система має кінцеве число станів – 2, тобто даний процес буде дискретним. Оскільки стан системи залежить від її стану зараз і не залежить від того, як система потрапила у цей стан, процес марковський. Побудуємо граф станів роботи системи (рис. 5.4).

Рисунок 5.4 – Граф станів роботи системи

Розглянемо інтервал часу з 10.00 до 11.00. Нехай з 10.00 до 10.30 вікно обслуговує відвідувачів, з 10.30 до 10.40 вікно вільне, з 10.40 до 11.00 – вікно зайняте. Побудуємо графічну реалізацію (рис. 5.5).

Рисунок 5.5 – Графічна реалізація випадкового процесу

Аналітична реалізація має вигляд:

ЛЕКЦІЯ 6 ДИСКРЕТНИЙ МАРКОВСЬКИЙ ПРОЦЕС З ДИСКРЕТНИМ ЧАСОМ. МОРКОВСЬКИЙ ОДНОРІДНИЙ ЛАНЦЮГ

6.1 Поняття дискретного Марковського процесу з дискретним часом

Визначення 6.1. Випадковий процес, що протікає у системі називається процесом з дискретним часом, якщо переходи системи зі стану в стан можуть здійснюватися тільки в наперед визначені моменти часу , які називаються кроками (етапами) цього процесу.

Між сусідніми кроками система зберігає свої стани.

Визначення 6.2. Випадковий процес, що протікає у системі, називається процесом з неперервним часом, якщо переходи системи зі стан в стан можливі у будь-які випадкові моменти часу.

Розглянемо Марковський дискретний процес з дискретним часом.

Нехай – можливі стани системи , яка перескакує з одного стану в інший у моменти часу .

Для моменту система знаходиться в стані , отже, даний процес можна розглядати як випадкову функцію кроків або їх номерів .

Таким чином, цей процес є випадковою послідовністю або ланцюгом.

Визначення 6.3. Випадкова послідовність називається марковським ланцюгом, якщо для кожного кроку ймовірність переходу з довільного стану в довільний стан не залежить від того, коли і як система опиниться у стані .

Система у будь-який момент часу може перебувати тільки в одному стані , отже, при кожному події несумісні й утворюють повну групу подій.

Нехай, наприклад, спостереження за системою з 1-го по 6-й крок показали, що з 1-го по 2-й крок вона знаходилася в стані , з 2-го по 3-й крок – в стані , з 3-го по 4-й крок – в стані , з 4-го по 5-й крок – в стані , з 5-го по 6-й крок – в стані .

Тоді реалізація цього процесу – це невипадковий ланцюг подій (рис. 6.1).

Рисунок 6.1 – Графічна реалізація випадкового процесу