5.1 Поняття дискретного марковського процесу. Графи станів системи

Розглянемо поняття системи.

Визначення 5.1. Під системою розуміють множину взаємозв’язаних елементів, які не можна розчленити на незалежні підмножини.

Якщо система змінює з часом свій стан випадковим чином, то говорять, що в системі протікає випадковий процес. Нехай – можливі стани системи , причому у будь-який момент часу система знаходиться в одному з них, тобто .

Якщо множина станів скінчена, то говорять, що вона дискретна, інакше – неперервна.

Якщо система має дискретну множину станів, то вона переходить зі стану в стан стрибком, якщо ж система має неперервну множину станів – то плавно.

Визначення 5.2. Випадковий процес, що протікає в системі , називається марковським, якщо йому властива відсутність післядії (тобто для кожного моменту часу ймовірність будь-якого стану системи в майбутньому (при ) залежить від її стану в сьогоденні (при ) і не залежить від того, як і скільки часу розвивався цей процес у минулому.

Для аналізу дискретного випадкового процесу зручно користуватися графами станів системи.

Визначення 5.3. Під графом станів системи розуміють множину вузлів, що позначають стани системи, і множину гілок можливих безпосередніх переходів зі стану в стан.

Приклад графа станів показано на рисунку 5.1, де , – стани системи, гілки – дозволені переходи зі стану в стан.

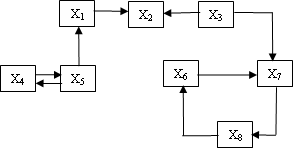
Рисунок 5.1 – Приклад графа станів системи

Відсутність гілок між станами говорить про неможливість переходу за один крок зі стану в стан.

Стани, у яких немає входу, називають станами без входу, стани, з яких немає виходу – станами без виходу (поглинаючими станами або пастками). Група станів без виходу називається множиною без виходу або нестійкою множиною. У наведеному прикладі (рис. 5.1) – стан без виходу, – поглинаючий стан, , – нестійка множина.

Визначення 5.4. Система називається ергодичною («ергос» – грець. – робота), якщо вона з будь-якого свого стану може за кінцеве число кроків перейти у будь-який інший стан.

Іншими словами, ергодична система повинна не мати станів і множин без входу і виходу. Приклад ергодичної системи показано на рисунку 5.2.

Рисунок 5.2 – Приклад графа станів ергодичної системи

При вивченні системи слід з’ясувати, в яких станах вона може знаходитися, які переходи зі стану в стан можливі й побудувати граф станів.

Щоб інтерпретувати як дискретну випадкову величину, потрібно кожен стан охарактеризувати кількісно. Для цього можна, наприклад, приписати кожному стану свій номер. Тоді , буде дискретною випадковою величиною з множиною значень 1, 2, 3.

Дискретну випадкову величину називають перетином випадкового процесу, що протікає в системі у момент часу .

Якщо провести спостереження за процесом, що протікає в системі протягом деякого проміжку часу від до ( ), то випадковий процес у кожен момент часу прийме конкретне числове значення, внаслідок чого отримаємо звичайну функцію, яка називається реалізацією випадкового процесу на тимчасовому проміжку .

Для однозначності вважатимемо, що у момент перескоку система знаходиться у стані, в який вона перескочила.