4.2 Властивості потоку подій
Розглянемо властивості, притаманні потокам подій.
1) Ординарність.
Визначення 4.2. Потік називається ординарним, якщо події в ньому з’являються поодинці, а не по два, по три тощо.
Ординарність
потоку означає, що ймовірність попадання
на елементарну ділянку
двох або більше подій досить мала в
порівнянні з ймовірністю попадання на
неї рівно однієї події, тобто при
ця ймовірність є нескінченно малою
вищого порядку. Нехай:
– імовірність
попадання на ділянку
рівно однієї події;
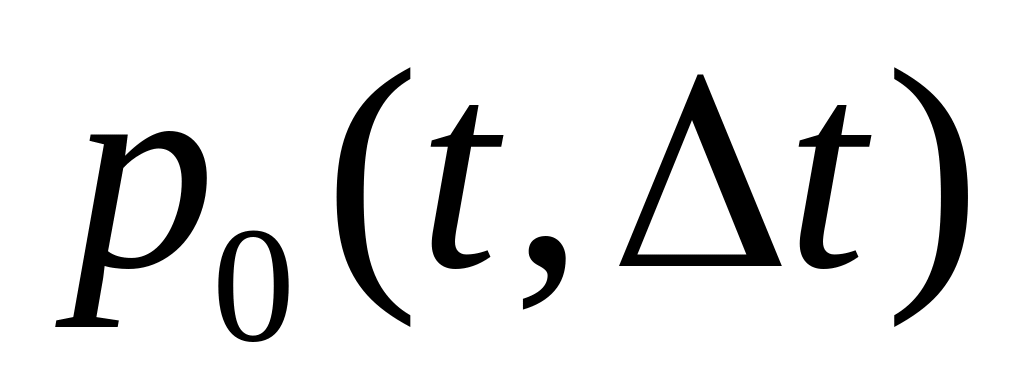– імовірність
не попадання на ділянку
жодної події;
–
імовірність
попадання на ділянку
двох або більше подій.
Тоді
як сума ймовірностей групи несумісних подій.
Для ординарного потоку подій ймовірність настільки мала в порівнянні з іншими доданками, що нею можна знехтувати.
або
Для ординарного потоку можна знехтувати можливістю одночасної появи на ділянці двох або більше подій.
Наведемо приклади ординарних потоків:
потік деталей, що надходять на конвеєр збірки;
потік автомобілів, що прибувають на станцію технічного обслуговування;
потік відмов технічного пристрою;
потік пасажирів, що підіймаються в ліфті на певний поверх.
Визначення
4.3. Інтенсивність
(щільність) ординарного потоку – це
межа відношення математичного сподівання
випадкової величини
числа подій, що потрапляють на елементарну
ділянку
до довжини цієї ділянки
.
Фізичний
зміст інтенсивності
потоку подій –
це
середнє число подій, що припадає на
одиницю часу елементарної ділянки
,
що примикає до
.
Інтенсивність
потоку подій
–
це
невід’ємна функція часу
,
яка має розмірність [1/год.].
Середнє
число подій ординарного потоку, що
приходиться на інтервал часу
,
що примикає до точки
,
дорівнює
,
А при постійній інтенсивності потоку
2) Відсутність післядії.
Визначення 4.3. Потік подій називається потоком без післядії, якщо ймовірність попадання будь-якого числа подій на одну з ділянок не залежить від того, скільки їх потрапило на інші ділянки.
Для
будь-якого моменту часу
майбутні моменти настання потоку подій
(при
)
не залежить від того , в які моменти
наступали події у минулому (при
).
Якщо
потік без післядії, ординарний і має
постійну інтенсивність
,
то число подій
,
що потрапляють на ділянку
,
має розподіл Пуассона параметром
.
Якщо
,
тоді число подій
,
потрапляють на ділянку довжини
,
також розподілено за законом Пуассона,
але параметр
у цьому випадку не залежить від довжини
ділянки
і місця її розташування.
.
Розподіл у цьому випадку має вигляд:
Визначення 4.4. Ординарний потік подій, у якому відсутня післядія, називається пуассонівським потоком.
3) Стаціонарність.
Визначення 4.5. Потік називається стаціонарним, якщо його ймовірністні характеристики не змінюються з часом.
Для стаціонарного потоку подій попадання того чи іншого числа на ділянку довжини залежить тільки від довжини цієї ділянки (не залежить від того, де саме на осі часу ця ділянка розташована).
Іншими
словами, кількість подій
і
,
що потрапляють на дві ділянки однакової
довжини, матимуть однаковий розподіл.
Для стаціонарного потоку подій його
інтенсивність
постійна.
.
Визначення 4.6. Ординарний стаціонарний потік без післядії називається простим або стаціонарним пуассонівським потоком.
Імовірність
того, що за проміжок часу
завжди наступить
подій
Визначення 4.7. Потоком з обмеженою післядією називається потік, у якому випадкові інтервали між сусідніми за часом подіями є незалежними випадковими величинами.
Визначення 4.8. Стаціонарний потік з обмеженою післядії, в якому інтервали є послідовністю незалежних однаково розподілених випадкових величин, називається потоком Пальма.
Наведемо приклади потоків Пальма:
моменти приходу автобуса на зупинку;
потік відмов технічного пристрою тощо.
Так, простий (стаціонарний пуассонівський) потік є потоком Пальма, але це не означає, що потік Пальма завжди є простим потоком.
4) Регулярність.
Визначення 4.9. Потік подій, у якому інтервали між подіями однакові і рівні невипадковій величині, називається регулярним.
Наведемо приклади регулярних потоків:
потік зміни цифр хвилин на вокзальному електронному годиннику;
потік змін станів ЕОМ, визначені тактом її роботи тощо.
Схематично такий потік зображено на рисунку 4.3.
Рисунок 4.3 – Регулярний потік подій
ЛЕКЦІЯ 5 ДИСКРЕТНИЙ МАРКОВСЬКИЙ ПРОЦЕС