3.1 Визначення числових характеристик випадкових процесів

Випадковий процес при даному визначається щільністю ймовірності . Очевидно, що щільність не є вичерпним описом випадкового процесу , бо вона не виражає залежності між його перерізами у різні моменти часу.

Як вже говорилося, випадковий процес визначається сукупністю всіх перерізів при будь-яких значеннях , тому для його опису необхідно розглядати багатовимірну випадкову величину , що складається із усіх перерізів його процесу. У загальному випадку таких перерізів нескінченна множина, але для опису випадкового процесу вдається обійтися відносно невеликою кількістю перерізів.

Говорять, що випадковий процес має порядок , якщо він повністю визначається щільністю сумісного розподілу довільних перерізів процесу, тобто щільністю -мірної випадкової величини , де – переріз випадкового процесу у момент часу , .

Випадковий процес може бути описаний числовими характеристиками:

• математичним сподіванням;

• дисперсією або середньоквадратичним відхиленням;

• кореляційною функцією;

• нормованою кореляційною функцією.

Визначення 3.1. Математичним сподіванням випадкового процесу називається невипадкова функція , яка при будь-якому значенні змінної дорівнює математичному сподіванню відповідного перерізу випадкового процесу , тобто .

Математичне сподівання випадкового процесу має наступні властивості:

1. математичне сподівання невипадкової функції дорівнює самій невипадковій функції

;

2. невипадковий множник можна виносити за знак математичного сподівання

;

3) математичне сподівання суми двох випадкових функцій дорівнює сумі математичних сподівань доданків

;

4) для того, щоб знайти математичне сподівання суми випадкової і невипадкової функції, достатньо до математичного сподівання випадкової функції додати невипадкову функцію

.

Приклад 3.1. Знайти математичне сподівання випадкової функції , де – випадкова величина, – невипадкова функція, а .

Розв’язування. .

Визначення 3.2. Дисперсією випадкового процесу називається невипадкова функція , яка при будь-якому значенні змінної дорівнює дисперсії відповідного перерізу випадкового процесу , тобто .

Дисперсії випадкової функції притаманні наступні властивості:

1) Дисперсія невипадкової функції дорівнює нулю

;

2) Дисперсія суми випадкової функції і невипадкової функції дорівнює дисперсії випадкової функції

;

3) Дисперсія добутку випадкової функції та невипадкової функції дорівнює добутку квадрата невипадкового множника та дисперсії випадкової функції

.

Приклад 3.2. Знайти дисперсію випадкової функції , якщо , де – випадкова величина, – невипадкова функція, а .

Розв’язування. .

Визначення 3.3. Середньоквадратичним відхиленням випадкового процесу називається арифметичне значення кореня квадратного з його дисперсії, тобто .

Математичне сподівання випадкового процесу характеризує середню траєкторію усіх можливих його реалізацій, а його дисперсія або середньоквадратичне відхилення – розсіювання реалізацій щодо середньої траєкторії.

На рисунку 3.1 схематичне зображено .

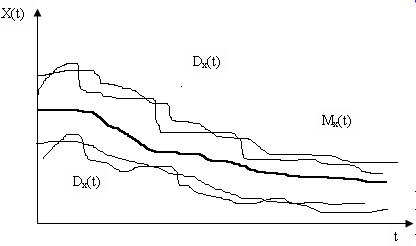
Рисунок 3.1 – Схематичне зображення

Функції є важливими числовими характеристиками, але вони не дають повної інформації про поводження випадкового процесу . Зустрічаються випадки, коли два випадкові процеси мають однакові , але за своєю внутрішньою структурою вони істотно різні. Наприклад, цю відмінність показано на рисунку 3.2, 3.3, де зображено два випадкові процеси з приблизно однаковими математичними сподіваннями та дисперсіями. Якщо для процесу характерна повільна зміна значень реалізації зі зміною , то для випадкового процесу ця зміна відбувається значно швидше. Іншими словами, для випадкового процесу характерна тісна ймовірнісна залежність між двома його перерізами та , тоді як для випадкового процесу ця залежність між перерізами та практично відсутня. Вказана залежність між перерізами характеризується кореляційною функцією.

Рисунок 3.2 – Схематичне зображення процесу

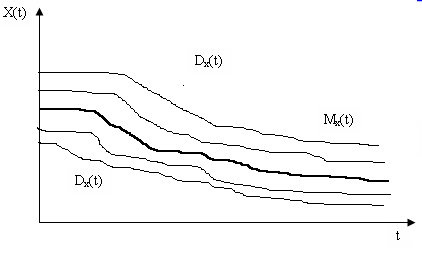
Рисунок 3.3 – Схематичне зображення процесу

Визначення 3.4. Кореляційною функцією випадкового процесу називається невипадкова функція двох змінних та , яка при кожній парі змінних та дорівнює коваріації відповідних перетинів та випадкового процесу.

.

Властивості кореляційної функції.