2.2 Закони розподілу випадкових процесів

Універсальною характеристикою випадкової величини є її функція розподілу.

– імовірність того, що випадкова величина прийме значення менше заданого . Нехай є випадковий процес . Перетин випадкового процесу при будь-якому фіксованому значенні аргументу – це випадкова величина зі своїм законом розподілу

, причому називається законом розподілу випадкового процесу . Ця функція характеризує властивості одного перетину , але не дає уявлення про сумісний розподіл двох або більше перетинів (рис. 2.2).

Рисунок 2.2 – Реалізація випадкового процесу

Функція називається одномірним законом розподілу випадкового процесу і характеризує лише властивості одного, окремо вибраного перерізу випадкового процесу .

Розглянемо два випадкові процеси, подані реалізаціями (рис. 2.3, 2.4).

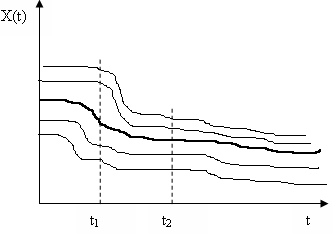
Рисунок 2.3 – Випадковий процес

Рисунок 2.4 – Випадковий процес

Якщо реалізації випадкового процесу мають плавний характер, то для ми спостерігаємо різкі зміни реалізації. Для процесу характерна тісна залежність між перерізами випадкового процесу, тоді як для тіснота цієї залежності зменшується зі збільшенням відстані між перерізами. Отже, не дає повної інформації про випадковий процес.

Повнішою характеристикою випадкового процесу є двовимірний закон розподілу, представлений суміжною функцією розподілу двох перетинів для та (рис. 2.5).

.

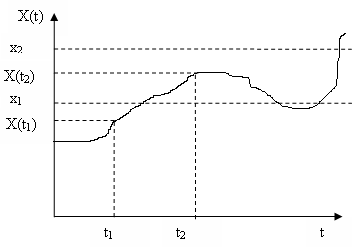
Рисунок 2.5 – Реалізація випадкового процесу і два його перерізи

Таким чином, ми дістали функцію чотирьох аргументів . Тривимірний закон розподілу має вигляд:

.

Теоретично можна необмежено збільшувати кількість перерізів і діставати при цьому повну інформацію про випадковий процес . Але оперувати такими функціями, які залежать від багатьох аргументів, дуже незручно. На практиці обмежуються одно- і двовимірним законом розподілу випадкового процесу або його числовими характеристиками – математичним сподіванням, дисперсією або середньоквадратичним відхиленням, кореляційною функцією, нормованою кореляційною функцією.

Якщо ж відомий характер процесу та закон його розподілу, то виходять з наступних міркувань.

1) Якщо випадковий процес дискретний, то його математичне сподівання визначається за формулою:

.

2) Якщо неперервний і відома щільність розподілу , то за формулою:

.

3) Дисперсія неперервного випадкового процесу зі щільністю розподілу дорівнює

або

.

2. 3 Елементарні випадкові функції

У реальних задачах випадкові процеси зручно подавати у вигляді найпростіших елементарних функцій.

Визначення 2.8. Елементарною випадковою функцією називається така функція від аргументу , в якій залежність від подається звичайною невипадковою функцією, причому як параметри туди входять одна або кілька звичайних, незалежних від випадкових величин.

Наприклад, функція , де – неперервна випадкова величина, яка розподілена рівномірно в інтервалі [-1; 1] є елементарною випадковою функцією.

Приклад 2.1. Задана елементарна випадкова функція, де – випадкова величина, розподілена за законом . Визначити характеристики .

Розв’язання. Знайдемо математичне сподівання, дисперсію, середньоквадратичне відхилення, нормовану кореляційну функцію.

1) Математичне сподівання .

2) Для знаходження кореляції функції скористаємося формулами:

та

Отже,

При кореляційна функція дорівнює дисперсії

3) Середньоквадратичне відхилення.

4) Визначимо нормовану кореляційну функцію .

ЛЕКЦІЯ 3 ЧИСЛОВІ ХАРАКТЕРИСТИКИ ВИПАДКОВИХ ПРОЦЕСІВ