1.3 Роль прикладних економіко-математичних досліджень

Можна виділити щонайменше чотири функції щодо застосування математичних методів і моделей у вирішенні практичних задач:

• удосконалення системи економічної інформації;

• розв’язання принципово нових економічних задач;

• поглиблення кількісного аналізу економічних проблем;

• інтенсифікація і підвищення точності економічних розрахунків.

Математичні методи та моделі дозволяють упорядковувати систему економічної інформації, виявляти недоліки у наявній інформації і формувати вимоги до підготовки нової інформації чи її корегування. Розробка і застосування економіко-математичних моделей вказує шляхи вдосконалення економічної інформації, орієнтованої на вирішення певної системи завдань планування та управління. Прогрес у інформаційному забезпеченні планування та управління спирається на технічні та програмні засоби інформатики, яка бурхливо розвивається.

Формалізація економічних задач і застосування комп’ютерів прискорюють типові, масові розрахунки, підвищують точність і скорочують трудомісткість, дозволяють проводити багатоваріантні економічні дослідження та обґрунтування складних заходів.

Завдяки застосуванню економіко-математичного моделювання значно посилюються можливості кількісного аналізу, вивчення багатьох чинників, які впливають на економічні процеси, кількісна оцінка наслідків змін умов розвитку економічних об’єктів тощо.

За допомогою математичного моделювання вдається розв’язати такі економічні задачі, які іншими засобами розв’язати практично неможливо, наприклад, знаходження оптимального варіанта народногосподарського плану, імітація народногосподарських заходів, автоматизація контролю за функціонуванням складних економічних об’єктів.

Сфера практичного застосування економіко-математичного моделювання обмежується можливостями та ефективністю формалізації економічних проблем і ситуацій, а також станом інформаційного, математичного, технічного забезпечення використовуваних моделей. Намагання за будь-яку ціну застосувати математичну модель може не дати очікуваних результатів через відсутність необхідних умов.

Відповідно до сучасних уявлень щодо системи розробки і прийняття господарських рішень вона має поєднувати формальні та неформальні методи, які підсилюють один одного.

ЛЕКЦІЯ 2 ЗАКОНИ РОЗПОДІЛУ ВИПАДКОВИХ ПРОЦЕСІВ. ЕЛЕМЕНТАРНІ ВИПАДКОВІ ФУНКЦІЇ

2.1 Визначення випадкового процесу. Перерізи. Класифікація процесів

Теорія випадкових процесів (теорія випадкових функцій) є наукою, що вивчає закономірності випадкових подій (явищ) у динаміці їх розвитку.

У світі, що нас оточує, часто спостерігаються процеси, перебіг яких передбачити неможливо. Ця невизначеність зумовлюється впливом випадкових факторів на хід процесу. Наприклад, рівень води в річці або водосховищі змінюється під впливом випадкових чинників залежно від погоди, кількості опадів, інтенсивності зрошувальних заходів; напруга в електромережі відхиляється від номіналу під впливом таких випадкових факторів, як кількість увімкнених приладів, моменти їх вмикання чи вимикання тощо.

Можна впевнитися, що в будь-якому процесі присутній елемент випадковості, який виявляється більшою чи меншою мірою залежно від його фізичної основи. Отже, детермінованих процесів у навколишньому світі не існує – на перебіг будь-якого процесу впливають численні фактори, які під час дослідження (моделювання) врахувати практично неможливо.

Теорія випадкових процесів широко застосовується, коли йдеться про вивчення економічних, екологічних, соціальних та технічних систем. Базуючись на цій теорії, створюють стохастичні моделі, що описують більшість видів господарської діяльності людини і дають змогу з певною ймовірністю прогнозувати ситуації, які можуть виникати внаслідок цієї діяльності.

Випадковий процес пов’язаний з часом t. Тому у загальному випадку випадкові процеси позначають , де – випадкова подія. – простір елементарних подій, .

Визначення 2.1. Випадковим процесом називається процес, значення якого при будь-якому значенні аргументу t є випадковою величиною.

Іншими словами, випадковий процес є функцією, яка у результаті випробування може приймати той чи інший конкретний вигляд, невідомий заздалегідь. При фіксованому , – є звичайною випадковою величиною, тобто перетином випадкового процесу в момент .

Визначення 2.2. Реалізацією випадкового процесу називається невипадкова функція , на яку перетворюється випадковий процес у результаті випробування (при фіксованому ), тобто конкретний вигляд, що приймає випадковий процес , його траєкторія.

Таким чином, випадковому процесу притаманні риси випадкової величини, так і риси функції. Якщо зафіксувати значення аргументу , випадковий процес перетворюється на звичайну випадкову величину, якщо ж зафіксувати , то у результаті кожного випробування випадковий процес перетворюється на звичайну невипадкову функцію.

Надалі опустимо аргумент , але він матиметься на увазі.

Той факт, що у деякому експерименті випадковий процес здійснився, записуємо так , де уже не є випадковим процесом, і його залежність від набуває цілком певного вигляду.

Отже, – не випадкова функція. Таким чином, провівши експеримент, дістанемо деяку реалізацію випадкового процесу .

Визначення 2.3. Кожна реалізація випадкового процесу являє собою невипадкову функцію , на яку перетворюється випадковий процес у результаті проведення експерименту (опитування, спостереження).

Здійснивши не один експеримент, а кілька, дістанемо деяку множину реалізацій випадкового процесу.

Схематично це можна проілюструвати графіками, наведеними на рисунку 2.1.

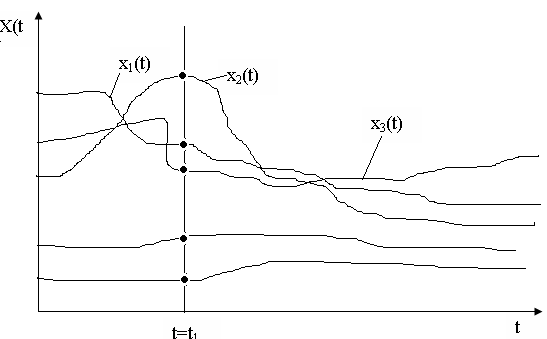
Рисунок 2.1 – Сім’я реалізацій випадкового процесу

– реалізації, вони різняться між собою. Якщо проведемо переріз при , то дістанемо випадкову величину, спостережувані значення якої позначено точками на вертикальній прямій, проведеній через .

Випадкова величина , яку дістанемо, проводячи переріз , є фіксацією випадкового процесу у даний момент часу.

Визначення 2.4. Випадкова величина , в яку реалізувався випадковий процес при значення аргументу , називається перерізом цього процесу.

Таким чином, випадковий процес є системою випадкових величин усіх перерізів процесу.

Отже, функції є стохастичними, тоді як є динамічним унаслідок зміни .

Перерізів може бути нескінченна множина. Тому досліджувати утворювану систему випадкових величин неможливо. У реальних задачах обмежуються двома чи трьома перерізами.

Випадкові процеси можна класифікувати за часом і за станами.

Визначення 2.5. Випадковий процес називається процесом із дискретним часом, якщо система, в якій він відбувається, може змінювати свої стани лише у фіксовані моменти часу , кількість яких скінчена або злічена.

Множина моментів переходу системи є зліченою і дискретною.

Приклади випадкових процесів із дискретним часом:

• процес роботи технічних систем, які підлягають огляду у момент часу 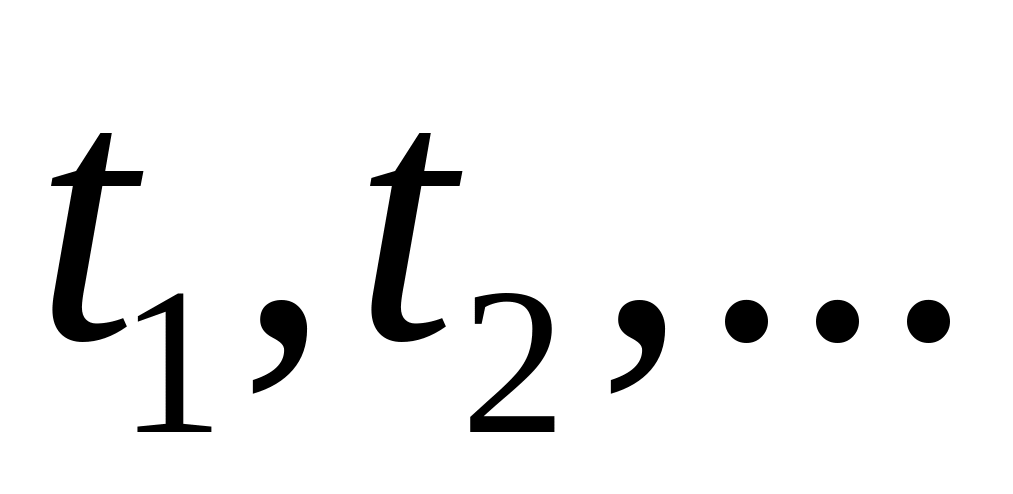і які потім переводять із однієї категорії придатності до експлуатації до експлуатації до іншої системи;

• процес роботи обчислювального центру, що може змінювати свої стани в моменти часу та ін.

Визначення 2.6. Випадковий процес називається процесом із неперервним часом, якщо переходи системи із одного стану до іншого можуть здійснюватися у будь-який момент часу .

Для випадкового процесу з неперервним часом множина моментів переходу системи із одного стану до іншого є незліченою.

Приклади випадкових процесів із неперервним часом:

• – кількість відказів у роботі технічного пристрою;

• – кількість осіб, які захворіли на грип у деякому місті у період епідемії, тощо.

Визначення 2.7. Випадковий процес називається процесом із дискретним станом, якщо у будь-який момент часу перерізом його є дискретна випадкова величина.

Наведемо приклади процесів із дискретними станами:

• у певні моменти часу вимірюється температура повітря у деякій місцевості. Послідовність значень цієї величини є випадковим процесом із неперервним станом і дискретним часом;

• процес зміни напруги в електромережі являє собою випадковий процес із неперервним станом і неперервним часом;

• технічний прилад містить 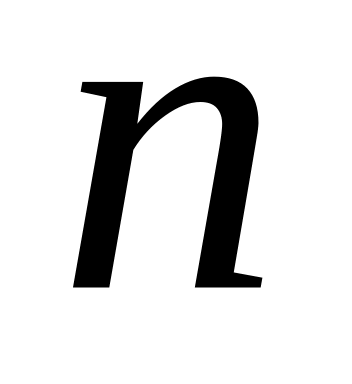елементів, які працюють незалежно один від одного і у процесі роботи можуть виходити із ладу. Випадковий процес – кількість елементів, які можуть вийти з ладу, є процесом із дискретним станом і неперервним часом.