11.1 Фінальний стаціонарний стан процесу
У застосуванні марковських процесів до фінансово-економічних ситуацій одним із важливих чинників є досить тривале протікання процесу, у тому числі протікання процесу після закінчення впливу на нього початкових умов. За деяких умов врешті-решт встановлюється фінальний стаціонарний режим процесу, при якому ймовірності станів системи вже не залежать ні від часу, ні від початкового розподілу ймовірностей.
Визначення
11.1.
Імовірності
станів системи у фінальному стаціонарному
стані системи називаються фінальними
(граничними, стаціонарними) ймовірностями
і позначаються
,
а вектор
,
координати якого служать фінальні
ймовірності, називається фінальним
(граничним, стаціонарним) вектором.
Розглянемо випадок однорідного марковського ланцюга, тобто систему з дискретними станами і дискретним часом.
Теорема 11.1. Якщо існує фінальний стаціонарний режим, і, отже, фінальні ймовірності, то для того, щоб були фінальними ймовірностями необхідно і достатньо, щоб існував -й крок такий, що
|
(11.1) |
.
Доведення.
Достатність.
Нехай існує фінальна ймовірність і
натуральне число
,
для якого виконується рівність (11.1).
Тоді при
з теореми, що для однорідного марковського
ланцюга вектор-рядок імовірностей
станів від
-го
до
-го
кроку дорівнює добутку вектора-рядка
ймовірностей станів від
-го
до
-го
кроку та матриці перехідних ймовірностей
. |
(11.2) |
Отже, з цієї теореми ми маємо, що при
Аналогічно
тощо.
Таким чином
,
тобто вектор не залежить від номеру кроку, а значить, є вектором фінальної ймовірності.
Необхідність. Нехай – фінальні ймовірності, тоді з визначення випливає, що знайдеться такий крок, починаючи з якого ймовірності станів не мінятимуться, тобто будуть фінальними, а це означає виконання рівності (11.1).
Наслідок. Якщо існують фінальні ймовірності, то для того, щоб були фінальними необхідно і достатньо, щоб існував -й крок такий, що
Доведення очевидне. При цьому фінальні ймовірності задовольняють умові нормування
.
Теорема 11.2. Якщо існують фінальні ймовірності, то фінальний вектор можна з рівняння
|
(11.3) |
,
де – матриця перехідної ймовірності.
Доведення. Оскільки фінальні ймовірності існують, то знайдеться натуральне число , що виконується рівність (11.1). Тоді з (11.2) при маємо
,
тобто рівність (11.3) доведено.
Визначення
11.2. Марковський
ланцюг називається регулярним, якщо
існує натуральне число
,
таке, що будь-який елемент матриці
позитивний, окрім, можливо, елементів,
що стоять в стовпцях, номери яких
співпадають з нестійкими станами системи
,
тобто станами без входів.
Приклад 11.1. Розглянемо однорідний марковський ланцюг, розмічений граф станів, який представлений на рисунку 11.1.
Рисунок 11.1 – Розмічений граф станів
У даному випадку система не має нестійких станів. Запишемо матрицю перехідних ймовірності .
.
Маємо
Звідси
зрозуміємо, що
і т.д.
Тобто,
будь-яка
-ий
ступінь
матриці
перехідних ймовірностей системи
містить нульові елементи. Оскільки у
системі
немає нестійких станів, то марковський
ланцюг не є регулярним.
Приведемо (без доведення) теорему, у якій сформульовані достатні умови існування граничних імовірностей.
Теорема
11.3. Якщо
однорідний марковський ланцюг із
скінченим скінченним числом
станів регулярний, то існують фінальні
ймовірності, причому
.
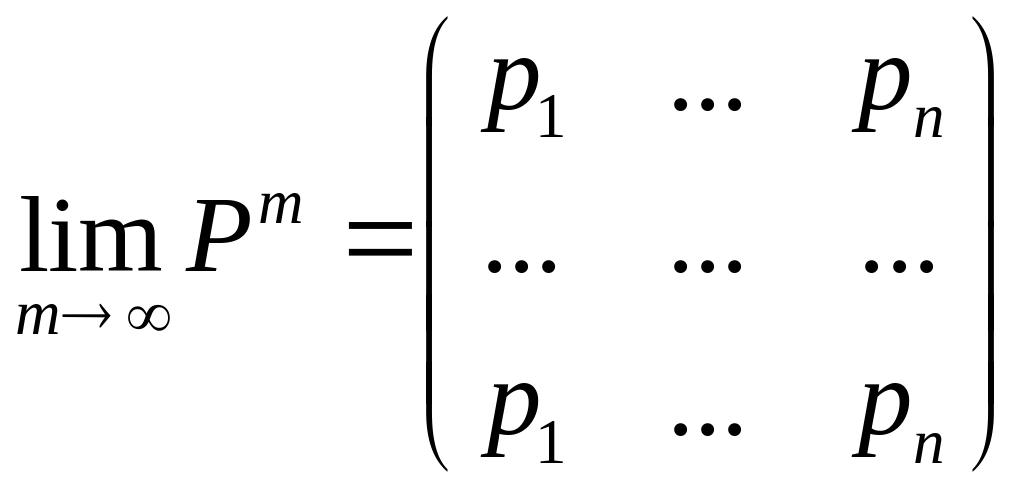Таким чином, для знаходження фінальних ймовірностей потрібно перевірити Марковський ланцюг на регулярність, і, якщо він є регулярним, фінальний вектор імовірностей можна знайти з рівняння (11.3).
Приклад 11.2. Розглянемо однорідний марковський ланцюг з розміченим графом (рис. 11.2). Визначити, чи є ланцюг регулярним і якщо так, знайти фінальні ймовірності.
Рисунок 11.2 – Розмічений граф станів
Розв’язання. Стан нестійкий. Запишемо матрицю перехідних імовірностей
.
Знайдемо
для з’ясування регулярності
.
При
кожен елемент матриці
,
за винятком елементів третього стовпця
номер якого співпадає з номером нестійкого
стану
,
позитивний. Отже, даний марковський
ланцюг регулярний, й існують фінальні
ймовірності
.
Знайдемо їх за формулою (11.3)
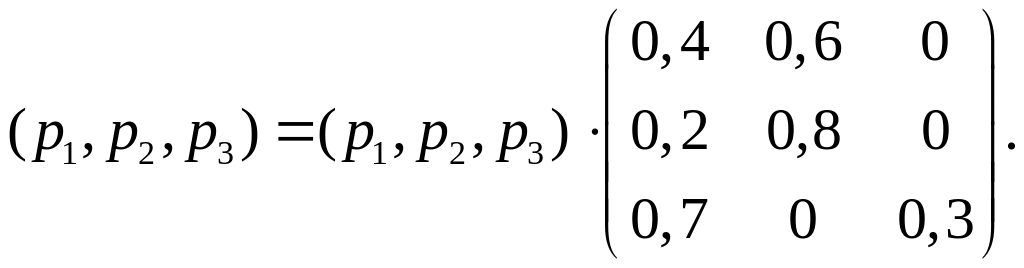
Провівши множення в правій частині цієї рівності, отримаємо
або в алгебраїчній формі
З першого
рівняння
Отже,
– загальний розв’язок рівняння, який
залежить від параметра
.
Знайдемо його з умови нормування
Тоді
.
Отже, вектор фінальних станів системи має вигляд
У прикладі гранична ймовірність нестійкого стану дорівнює нулю. Це справедливо в загальному випадку будь-якої системи.
Відзначимо, що у нерегулярного марковського ланцюга все ж таки можуть існувати граничні ймовірності. Нехай є система , граф станів якої зображений на рисунку 11.3
Рисунок 11.3 – Розмічений граф станів
Є
поглинальний стан
,
тому при
система перейде у цей стан і залишиться
у ньому назавжди. Отже, для даної системи
фінальні ймовірності існують і складають
.
Поте, дана система не є регулярною, оскільки стани і не є нестійкими, але елементи, що стоять на перетинах третього рядка і перших двох стовпців будь-якого ступеня матриці перехідних імовірностей
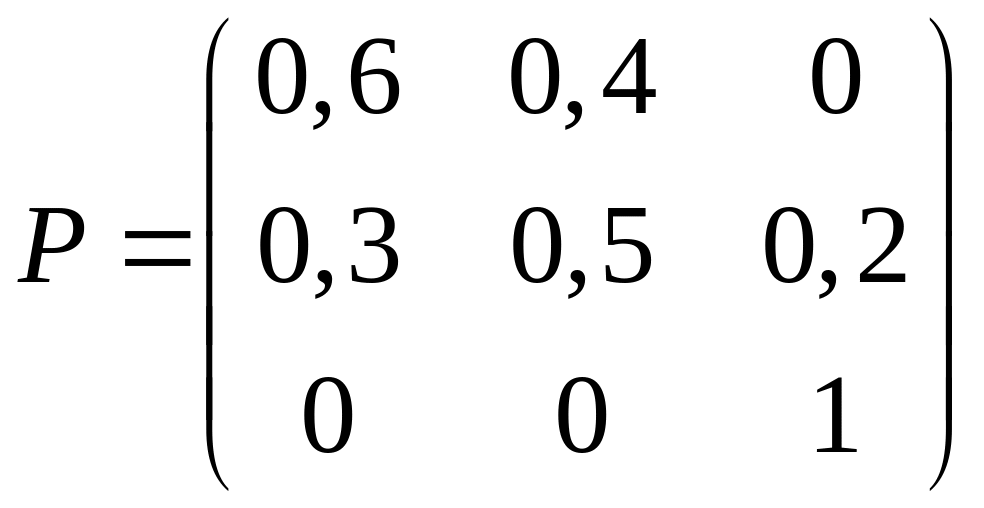
очевидно, будуть дорівнювати нулю.
ЛЕКЦІЯ 12 СИСТЕМИ МАСОВОГО ОБСЛУГОВУВАННЯ