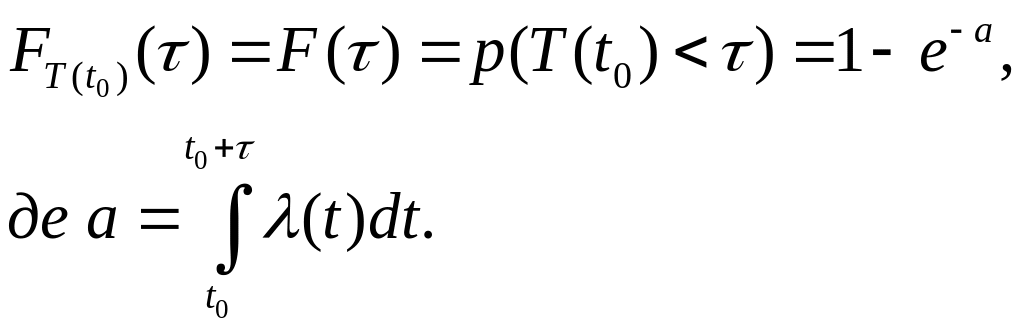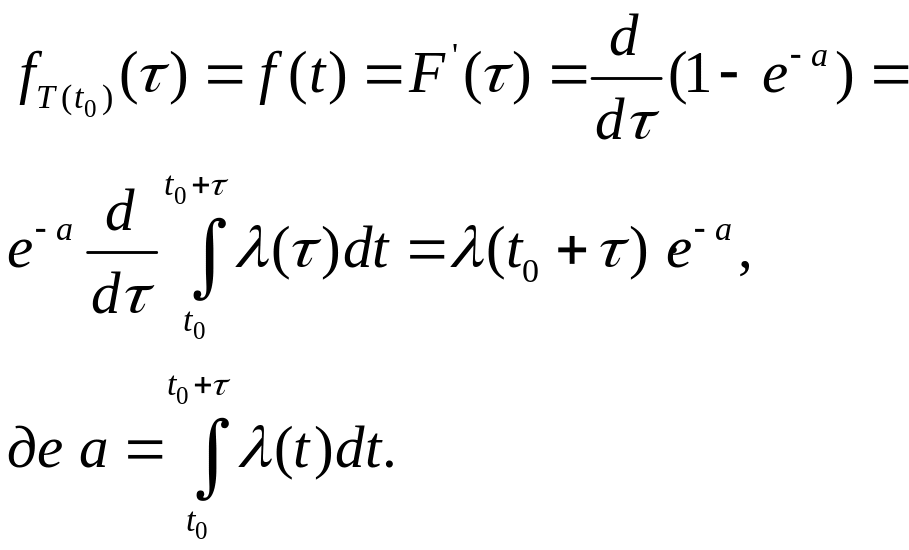10.2 Друга характеристика пуассоновського нестаціонарного потоку подій

Розглянемо випадкову величину – проміжок часу між двома сусідніми подіями в потоці, перша з яких наступила у момент часу .Ця неперервна випадкова величина буде розподілена вже не по показовому закону як величина , вид її закону розподілу залежатиме від та від функції . Формули характеристик наведемо у таблиці 10.2.

Таблиця 10.2 – Характеристики випадкової величини

Характеристика	Формула
Інтенсивність нестаціонарного пуассоновського потоку.
Інтегральна функція розподілу випадкової величини , тобто ймовірність того, що за проміжок часу між двома сусідніми подіями у потоці, перша з яких наступить у момент , буде менше .
Ймовірність того, що проміжок часу між двома сусідніми подіями у потоці, перша з яких наступить у момент , буде не менше .

Продовження таблиці 10.2

Диференціальна функція випадкової величини (тобто щільність розподілу).
Математичне сподівання (середнє значення) випадкової величини , тобто середній проміжок часу між двома сусідніми подіями в потоці, перша з яких наступить у момент .
Дисперсія випадкової величини .
Середньоквадратичне відхилення величини .	.

Приклад 10.1. Проаналізуємо потік надходжень вимоги за виплатами у страхову компанію відповідно до страхових полісів за період з початку листопада до кінця січня, розглянуту у прикладі 9.1 (лекція 9). Вивчення цього потоку за даний період у минулі роки показано, що число вимог за виплатами, що надходять у компанію за проміжок часу , залежить не тільки від його тривалості, але й від моменту його початку. Пояснюється це тим, що в даний період відбувається погіршення погоди (випадають опади, сніг, має місце ожеледиця), рано темніє, погіршується у зв’язку з цим обстановка на дорогах, це призводить до зростання дорожньо-транспортних пригод.

Незалежність надходжень вимог за виплатами у будь-які пересічні інтервали часу й надходження вимог поодинці в малі проміжки часу також зберігаються в даному випадку. Очікуване число вимог, що надходять в компанію за тиждень, залежить від часу таким чином .

Охарактеризуйте процес і з’ясуйте з якою ймовірністю:

1) протягом листопада в компанію надійде 6 вимог;

2) протягом грудня в компанію надійде 6 вимог;

3) протягом січня надійде не менше 5-ти вимог;

4) протягом перших двох тижнів не надійде жодної вимоги;

5) протягом другого та третього тижня грудня надійде хоча б одна вимога;

6) інтервал часу між двома сусідніми надходженнями вимог буде не менше з три дня, якщо перша з них поступила в перший день другого тижня січня;

7) інтервал часу між двома сусідніми надходженнями вимог буде не менше двох днів, якщо перша з них поступила на початку третього тижня грудня?

Розв’язок. Нехай П – потік вимог за виплатами, що надходять в страхову компанію. Так само як і в прикладі (лекція 9) робимо висновок про те, що потік П є ординарним потоком без післядії, тобто пуассоновським. Але даний потік вже не є стаціонарним, і, отже, вже не буде простим.

За одиницю часу приймемо тиждень (7 днів).

Нехай – випадкове число вимог, що поступили до компанії за проміжок часу [ ; ], – випадковий інтервал часу між двома сусідніми вимогами, перша з яких поступила у момент часу .

Відповімо на поставлені питання.

1) У першому тижні місяць = 4 тижні, момент початку цього проміжку (рис. 10.1).

Рисунок 10.1 – Розташування моментів початку проміжків

Математичне сподівання випадкової величини

.

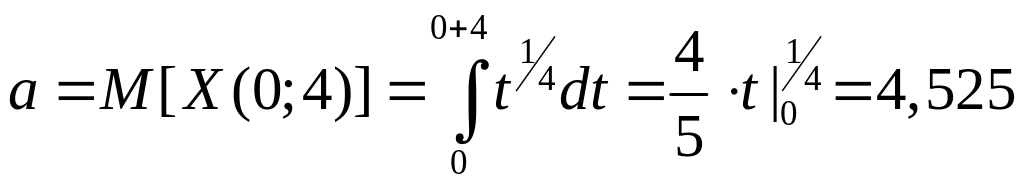За формулою 3-го рядка таблиці 10.1 можна підрахувати необхідну ймовірність випадкової величини

2) У другому питанні місяць = 4 тижні, , тоді за формулою другого рядка таблиці 10.1

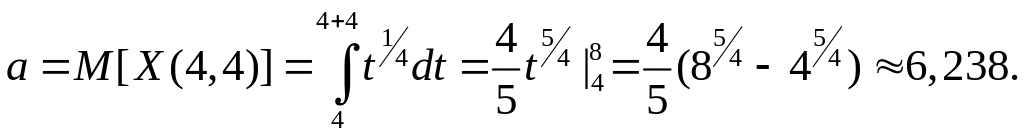
За формулою 3-го рядка таблиці 10.1

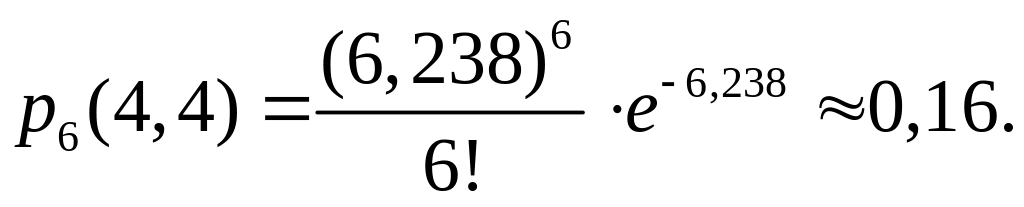
3) У третьому питанні місяць = 4 тижні, Тоді за формулою 2-го рядка таблиці 10.1

Шукану ймовірність обчислимо за формулою 6-го рядка таблиці 10.1

4) У четвертому питанні тижні, , . За формулою 2-го рядка таблиці 10.1

Тоді за формулою 4-го рядка таблиці 10.1

.

5) У п’ятому питанні тижні, За формулою 2-го рядка таблиці 10.1

Тоді за формулою 7-го рядка таблиці 10.1

.

6) У шостому питанні дні = тижня. За формулою 2-го рядка таблиці 10.1

Необхідну ймовірність обчислюємо за формулою 3-го рядка таблиці 10.2

.

7) У сьомому питанні дні = тижня. Математичне сподівання випадкової величини обчислюємо за формулою 2-го рядка таблиці 10.1

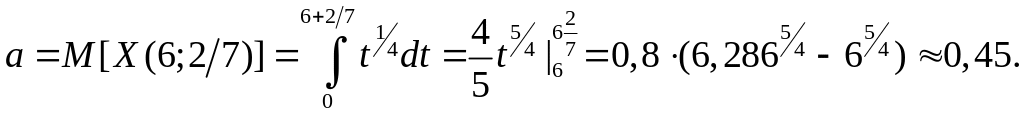
Тоді ймовірність того, що інтервал часу між двома сусідніми вимогами за виплатами, перша з яких поступила в компанію на початку третього тижня грудня, буде менше двох днів, дорівнює (2-й рядок таблиці 10.2)

.

ЛЕКЦІЯ 11 ФІНАЛЬНІ ЙМОВІРНОСТІ ОДНОРІДНОГО МАРКОВСЬКОГО ЛАНЦЮГА З ДИСКРЕТНИМ ЧАСОМ