8.3. Приклад дискретного марковського процесу з неперервним часом

Приклад 8.1. Для вивчення надійності експлуатації лічильника купюр, який приймемо за систему , розглянемо наступні стани:  лічильник справний,  лічильник справний і експлуатується,  лічильник несправний і ремонту не підлягає.

Припустимо, що лічильник купюр може вийти з ладу тільки під час експлуатації. На даному етапі вивчення ремонт несправного лічильника не передбачається (отже, стан є пасткою). Також вважатимемо, що зміни щільності ймовірностей переходів системи зі стану в стан настільки малі, що ними можна знехтувати, тобто щільність ймовірностей переходів практично не залежить від часу (особливо, якщо проміжок, протягом якого аналізуємо роботу лічильника купюр, не дуже великий).

Розглянемо граф станів системи (рис. 8.3).

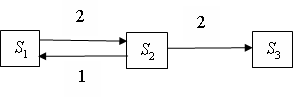
Рисунок 8.3 – Розмічений граф станів системи

Охарактеризувати процес і знайти ймовірності стану лічильника у момент часу , якщо у початковий момент лічильник знаходився в стані .

Розв’язання. Оскільки лічильник може міняти свої стани випадковим чином у випадкові моменти часу, а в кожен момент він перебуває в одному зі станів , то процес, що протікає у системі , буде дискретним випадковим процесом з неперервним часом. Даний процес можна вважати марковським, оскільки стан лічильника у майбутньому істотно залежить від його стану зараз і неістотно – від його станів у минулому. Незначні коливання щільності ймовірностей з часом дозволяють зробити припущення про однорідність даного процесу.

Матриця щільності ймовірностей переходів, складена за графом, має вигляд:

.

Знайдемо ймовірність станів для довільного . Для цього складемо систему диференціальних рівнянь Колмогорова.

(8.1)

Розглянемо два перші рівняння системи. Вони не містять функції , тому їх можна розглядати як систему двох рівнянь з двома змінними.

(*)

З теорії диференціальних рівнянь відомо, що пошук частинного розв’язку такої системи здійснюється у вигляді показникових функцій

,

(**)

де – постійні, які потрібно підібрати таким чином, щоб рівняння (**) задовольняли (*). Підставимо частинні розв’язки та в систему (*).

Продиференціюємо та поділимо обидва рівняння на .

(***)

Отримана однорідна лінійна система двох алгебраїчних рівнянь з невідомими та параметром, завжди має своїм розв’язком нульовий розв’язок , але який не задовольняє умові задачі, оскільки

А за початковими умовами .

Ненульовий розв’язок існує тоді і тільки тоді, коли її визначник дорівнює нулю

.

Це рівняння (відносно ) називається характеристичним рівнянням системи. Розкривши визначник, отримаємо квадратне рівняння відносно .

Корені знаходимо за теоремою Вієта або обчислюємо дискримінант.

Підставимо в (***) значення .

.

Таким чином отримали співвідношення, яке пов’язує . Оскільки – вільна невідома, то їй можна надати будь-яке числове значення, крім 0. Нехай , тоді . Підставимо у (**), отримаємо

(8.2)

Аналогічно обчислюємо для . Підставимо значення у (***).

.

Нехай , тоді (підставимо значення у (**)).

(8.3)

З (8.2) та (8.3) складаємо загальний розв’язок системи (8.1).

(8.4)

– довільні константи.

Щоб знайти частинний розв’язок системи (8.1), що задовольняю умовам , потрібно знайти відповідні значення .

Підставляємо в (8.4) ці значення і отримаємо шуканий частинний розв’язок, що задовольняє початковим умовам:

Для знаходження скористаємося умовою нормування:

Можна переконатися, що знайдені функції є ймовірнісними, тобто .

Підрахуємо ймовірність станів системи у момент часу , тобто .

Отже, ймовірність того, що у момент часу лічильник справний, але не експлуатується, ймовірність цього дорівнює 0,252; справний та експлуатується – з ймовірністю 0,234; несправний – з ймовірністю 0,514.

ЛЕКЦІЯ 9 ПУАССОНОВСЬКИЙ СТАЦІОНАРНИЙ (ПРОСТИЙ) ПОТІК ПОДІЙ