8.2. Однорідний дискретний марковський процес з неперервним часом

Розглянемо далі однорідний дискретний марковський процес з неперервним часом.

Граф станів марковського однорідного процесу з неперервним часом, у гілок якого вказані щільності ймовірностей переходів, називається розміченим.

На рисунку зображений граф станів системи, в якій протікає процес з неперервним часом (рис. 7.2).

Рисунок 8.2 – Розмічений граф станів системи

Відсутність на графі спрямованих гілок між певними станами означає, що щільність ймовірності відповідних переходів дорівнює 0. Наприклад, . Оскільки щільності ймовірностей переходів мають два індекси, то їх зручно розташувати у вигляді матриці

,

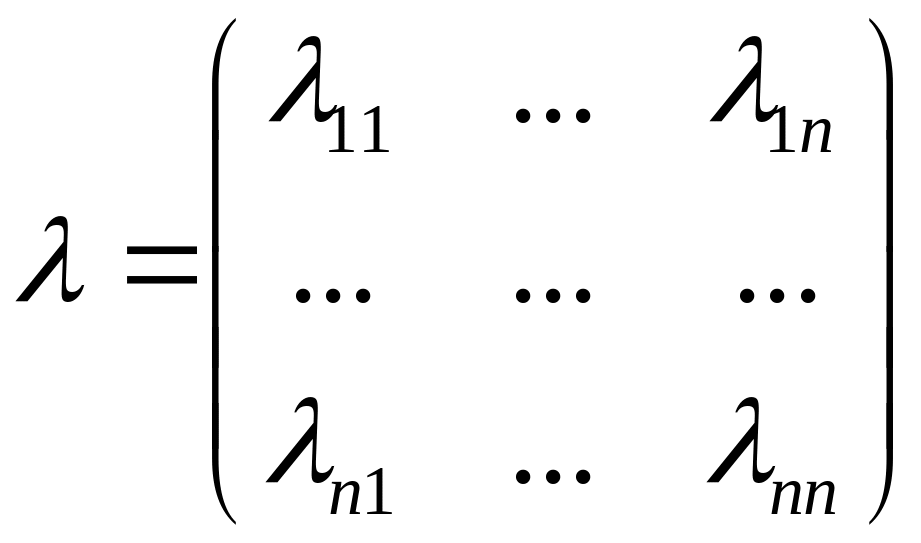причому .

Знаючи щільності ймовірностей переходів, можна скласти систему диференціальних рівнянь, щодо ймовірностей станів , а саме, справедлива наступна теорема.

Теорема 8.1. Ймовірність станів (невідомі ймовірнісні функції) є розв’язком наступної системи диференціальних рівнянь:

.

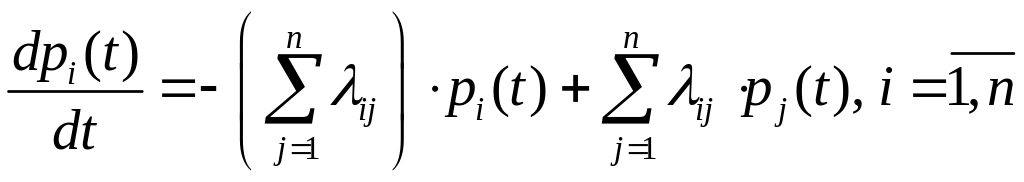Дану теорему довів відомий радянський математик Колмогоров А.М. (1093  1987). Саме він заклав основи теорії марковських випадкових процесів з неперервним часом і отримана ним система називається системою диференціальних рівнянь Колмогорова.

Оскільки шукані функції  функції однієї змінної, а саме, часу , то кожне рівняння є звичайним диференціальним рівнянням. Оскільки невідомі функції та їх похідні входять в рівняння тільки в першому ступені, то кожне рівняння системи називають лінійним.

Оскільки найвищий порядок похідних і шуканих функцій  перший, то рівняння системи є диференціальними першого порядку. Оскільки в кожному рівнянні системи вільні члени дорівнюють 0, то рівняння системи є однорідними. Нарешті, оскільки розглядаємо однорідний процес, то коефіцієнти в рівняннях постійні (щодо часу ).

Отже, система є системою звичайних однорідних диференціальних рівнянь першого порядку з постійними коефіцієнтами.

Якщо процес неоднорідний, то хоча б один з коефіцієнтів залежатиме від , у цьому випадку рівняння називають рівняннями зі змінними коефіцієнтами.

Скласти систему диференціальних рівнянь Колмогорова зручно по одному з наступних правил.

1) Правило складання диференціальних рівнянь Колмогорова за розміченим графом станів.

Для того, щоб скласти диференціальне рівняння Колмогорова для функцій , треба у лівій частині цього рівняння записати похідну функції , а в правій  добуток 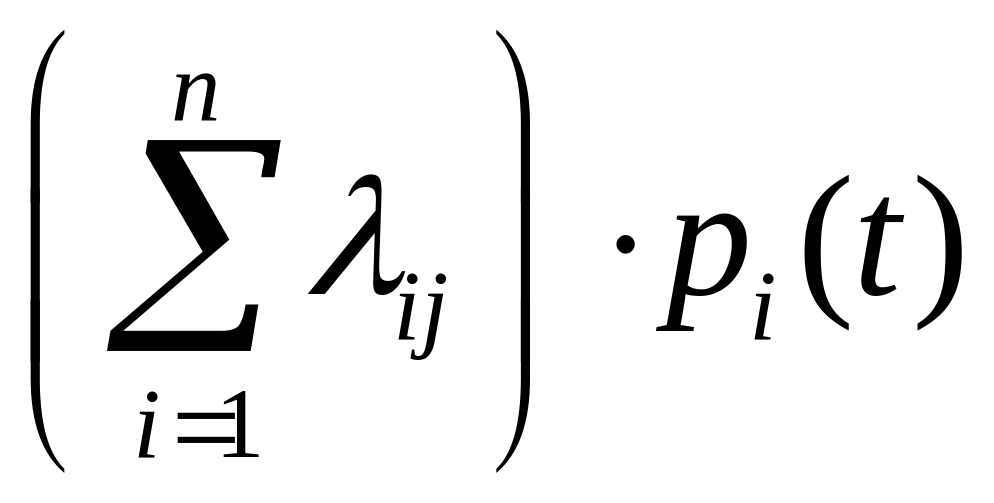суми щільності ймовірностей переходів для гілок, що виходять зі стану на ймовірність цього стану зі знаком мінус, плюс суму 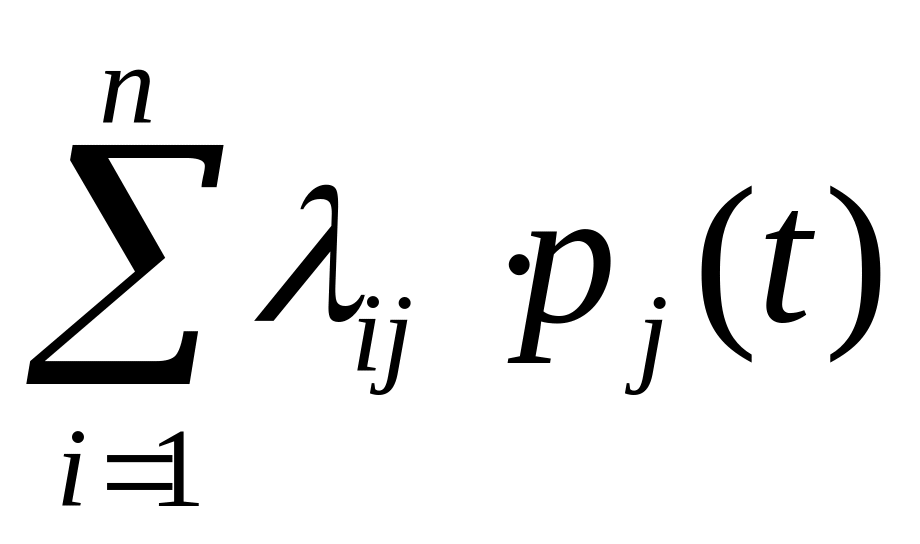, що входять до стану та ймовірностей станів , з яких ці гілки виходять. При цьому щільності ймовірностей переходів , відповідні відсутнім на графі гілкам, дорівнюють нулю.

Система диференціальних рівнянь Колмогорова, складена за розміченим графом, матиме наступний вид:

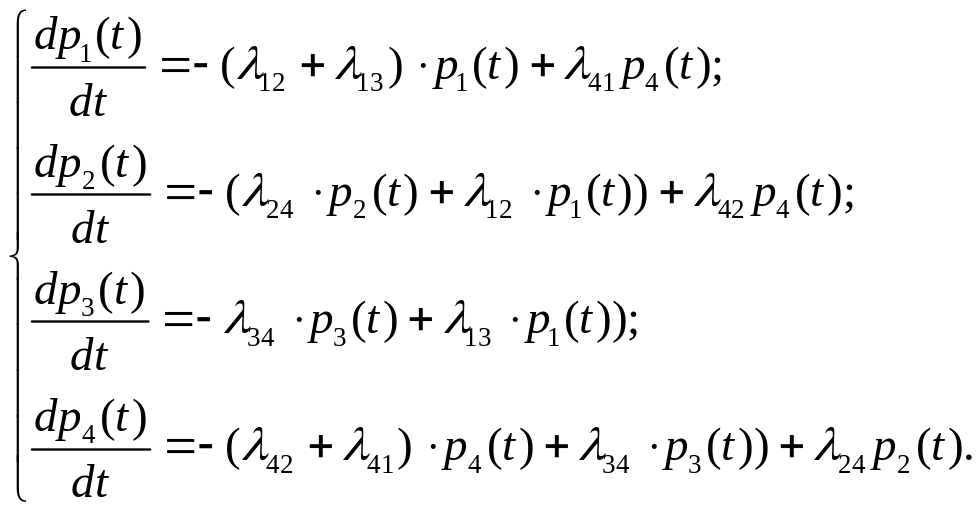
2) Правило складання диференціальних рівнянь Колмогорова за матрицею щільності ймовірності переходів.

Щоб скласти диференціальне рівняння Колмогорова для функції треба в лівій частині цього рівняння записати похідну функції , а в правій  добуток суми елементів -го рядка матриці та ймовірності стану (номер якого співпадає з номером обраного рядка) за знаком мінус, плюс суму добутків елементів -го стовпця та відповідної ймовірності .

Система диференціальних рівнянь Колмогорова складена, наприклад, за матрицею щільності ймовірностей переходів 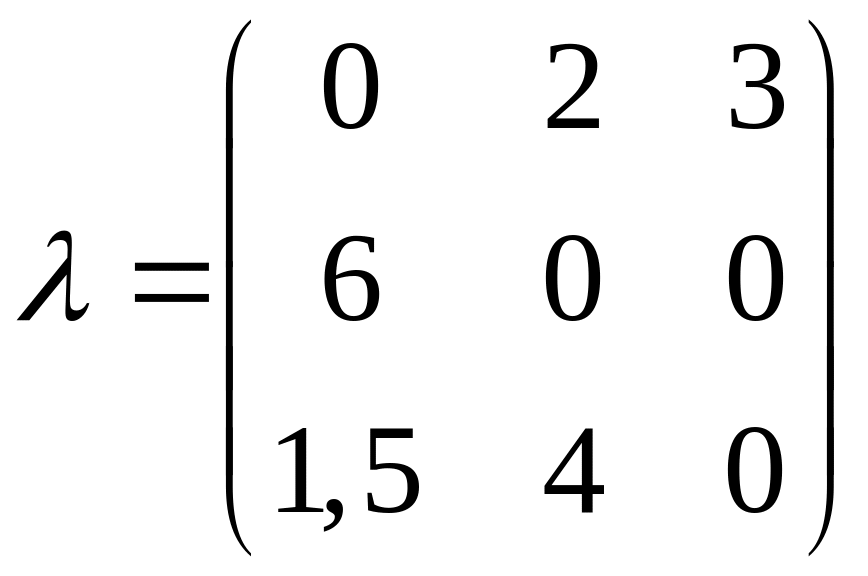має вигляд:

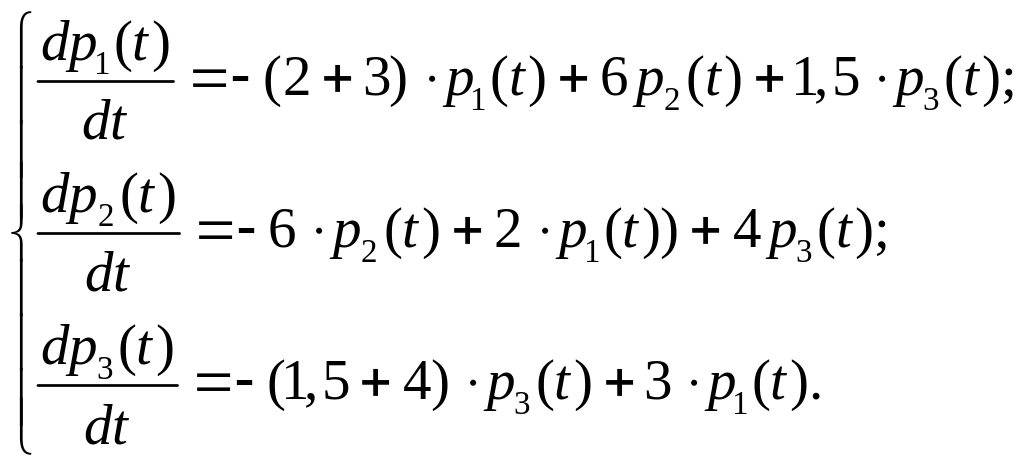
Початкові умови системи диференціальних рівнянь Колмогорова визначаються заданим розподілом ймовірностей станів системи в початкові моменти часу : і задовольняють умовам нормування

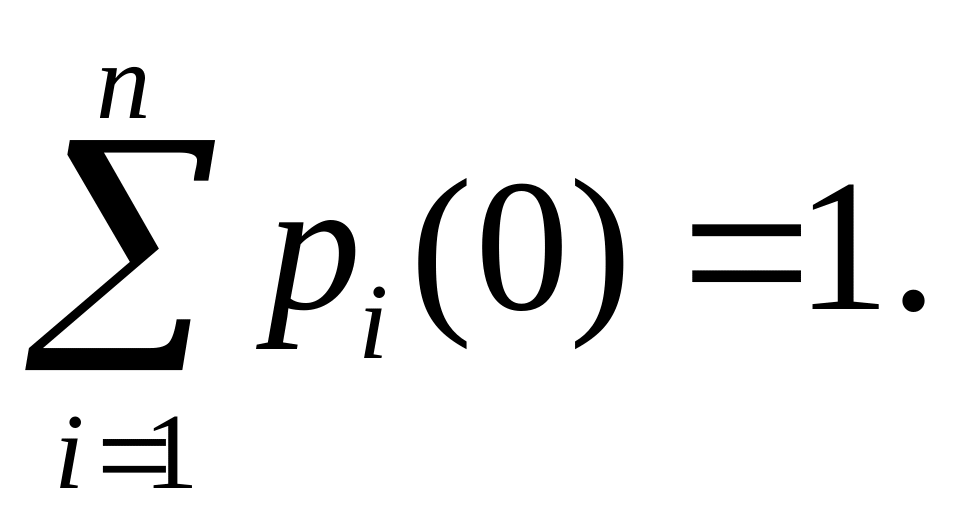
Якщо в початкові моменти часу система знаходиться в стані , то з урахуванням умови нормування отримуємо початковий розподіл ймовірностей

.

Система диференціальних рівнянь 1-го порядку, розв’язаних щодо похідних шуканих функцій, які входять до неї, називається системою, що має нормальну форму Коші.