7.1 Поняття марковського неоднорідного ланцюга

Визначення 7.1. Марковський ланцюг називається неоднорідним, якщо перехідні ймовірності (хоча б одна) залежать від номеру кроку . У цьому випадку перехідні ймовірності позначаються , а матриця перехідних ймовірностей залежить від :

.

При цьому матриця є стохастичною

.

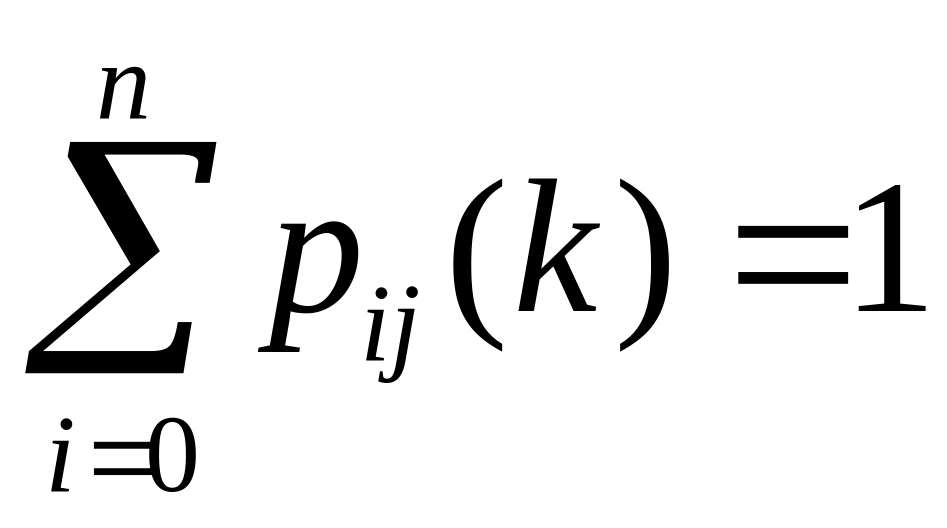Теорема 7.1. Для неоднорідного марковського ланцюга вектор-рядок ймовірностей станів від -го до -го кроку дорівнює добутку вектора-рядка ймовірностей станів від -го до -го кроку та матриці перехідних ймовірностей від -го до -го кроку

Наслідок. Для неоднорідного марковського ланцюга має місце формула

.

Доведення. Скористаємося теоремою.

Підставляючи у праву частину першого виразу значення для з другого виразу, отримаємо:

Продовжуючи обчислення аналогічним чином, отримаємо:

Приклад 7.1. Стани банку характеризуються однією з відсоткових ставок: 2%, 3%, 4%, які встановлені на початку кожного кварталу і фіксовані протягом кварталу. Якщо за систему прийняти банк, то вона в кожен момент часу може знаходитися тільки в одному з наступних трьох станів: – відсоткова ставка 2%, – відсоткова ставка 3%, – 4%. Нехай перехідні ймовірності залежать від моментів встановлення відсоткових ставок. Матриці перехідних ймовірностей задаються таким чином:

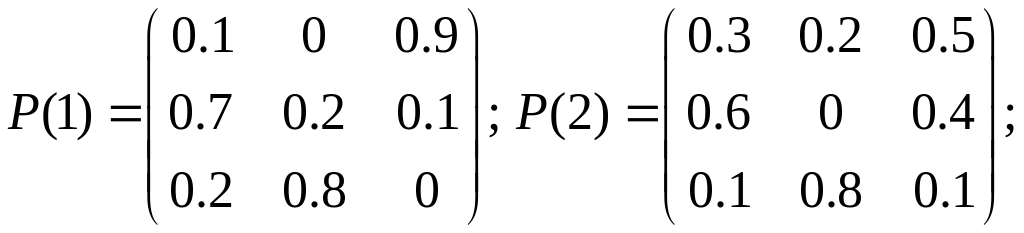
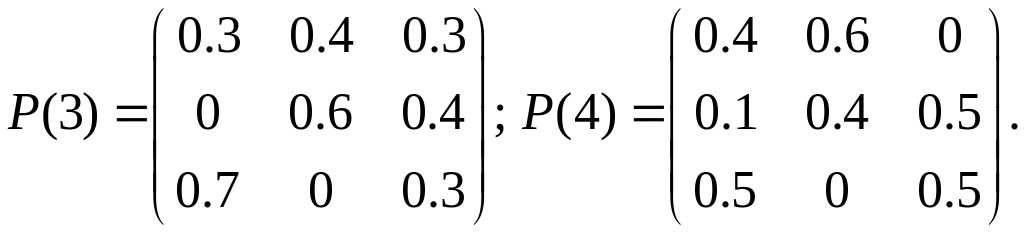
Знайти ймовірності станів банку наприкінці року, якщо наприкінці попереднього року ставка дорівнювала 4%. Охарактеризуйте процес.

Розв’язання. Оскільки за умовою перехідні ймовірності залежать від часу, то даний процес буде неоднорідний. Оскільки множина станів, у яких може знаходитися система кінцева (три стани), то випадковий процес, що протікає в системі дискретний. Даний процес є марковським, оскільки ймовірність перебування банку в одному зі своїх станів у майбутньому істотно залежить тільки від його стану зараз і не залежить від його станів у минулому.

Таким чином, у системі протікає неоднорідний марковський дискретний випадковий процес з дискретним часом, тобто маємо неоднорідний марковський ланцюг.

Оскільки наприкінці попереднього року відсоткова ставка складала 4%, то можна вважати, що у початковий момент система знаходиться у стані . Тому початковий розподіл ймовірностей має вигляд:

.

Ймовірності станів банку наприкінці року, тобто після чотирьох кварталів, можна знайти при та за формулою:

.

У результаті розрахунку отримаємо:

,

тобто наприкінці року ймовірності відсоткових ставок 2%, 3%, 4% складатиме відповідно 0,3584; 0,3696; 0,2720. Серед усіх ймовірностей число 0,3696 – найбільше. Таким чином, найімовірніша відсоткова ставка наприкінці року буде складати 3%.

Як контроль на правильність обчислень можна використовувати перевірку матриці на стохастичність.

ЛЕКЦІЯ 8 ДИСКРЕТНИЙ МАРКОВСЬКИЙ ПРОЦЕС З НЕПЕРЕРВНИМ ЧАСОМ

8.1 Випадкові процеси з неперервним часом. Поняття щільності ймовірності переходу системи в інший стан

На практиці часто зустрічаються випадкові процеси, в яких система змінює свої стани в будь-який випадковий момент часу  випадкові процеси з неперервним часом.

Нехай  можливі стани системи . Тоді ймовірністю -го стану системи в момент часу називається ймовірність

події , яка полягає у тому, що система у момент часу знаходиться у стані .

Марковський дискретний процес з неперервним часом вважається вивченим, якщо знайдені ймовірності всіх станів .

Оскільки в будь-який момент часу система може знаходитися тільки в одному зі станів , то події несумісні і утворюють повну групу. Тому (як відомо з теорії ймовірності) має місце умова нормування

.

Нехай  ймовірність переходу системи в момент часу зі станом в стан при та ймовірності затримки в момент часу в стані при . Якщо у момент часу система знаходиться в -му стані, то можна вважати, що точно у цей момент часу відбулася затримка системи в -му стані, тому . Тоді виходячи з умови нормування

,

можна зробити висновок, що ймовірність переходу системи з -го стану в інший -й стан точно в момент дорівнює нулю.

.

Тому ймовірності переходу у випадку процесу з неперервним станом вже не грають тієї визначальної ролі в обчисленні ймовірностей станів, яку вони виконували у випадку процесу з дискретним часом. Замість перехідних імовірностей у процесі з неперервним часом розглядають інші характеристики процесу  так звані щільності ймовірностей переходу зі стану в стан , які визначаються таким чином.

Позначимо через  ймовірність того, що система , що знаходилася у момент часу в стані за проміжок часу , (тобто за час ) перейде з нього в інший стан (рис. 7.1).

Рисунок 7.1 – Проміжок часу на осі часу

Рівність виконується у таких випадках:

• система у момент часу не знаходиться в стані ;

• система у момент часу знаходиться в стані , проте за проміжок часу 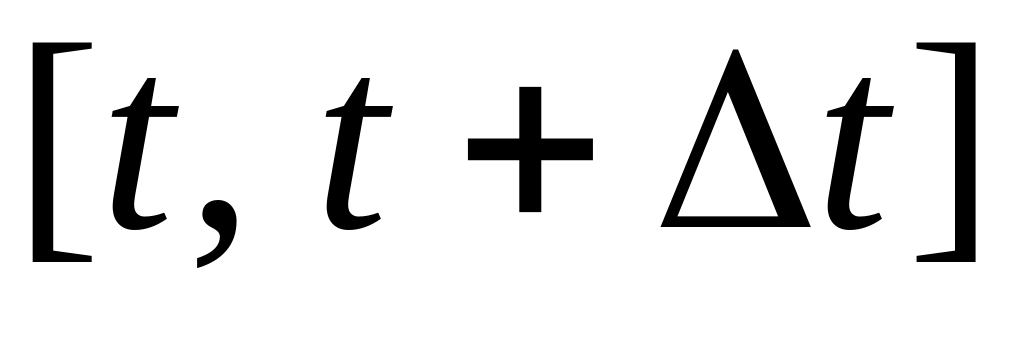вона перейшла в стан 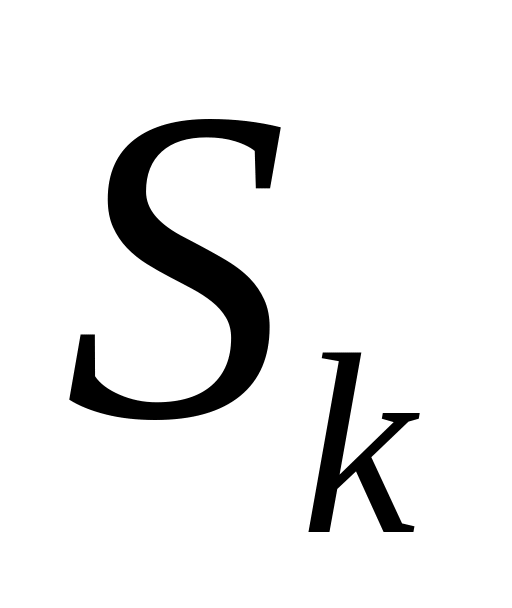, відмінний від стану ;

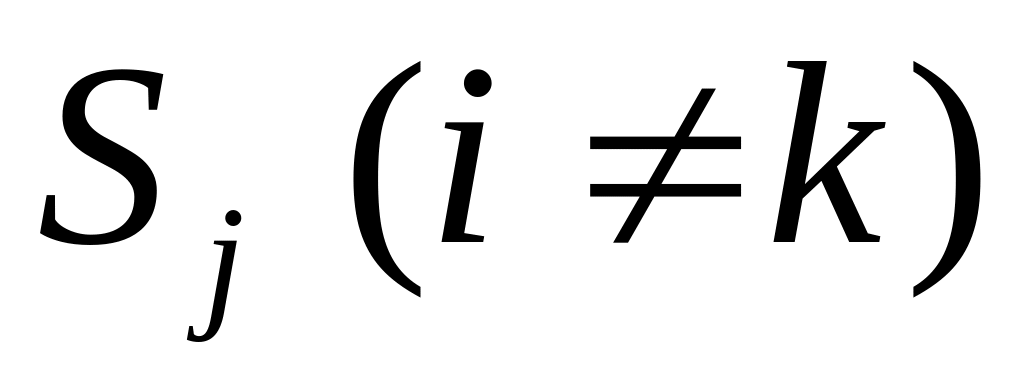• система у момент часу знаходиться в стані та залишається у цьому стані впродовж усього проміжку часу .

Для рівних індексів ймовірності переходу в інший стан втрачають змістовний сенс, і оскільки перехід в інший стан не здійснюється, то природно величини вважати рівними 0.

.

Визначення 8.1. Щільністю ймовірностей переходу системи зі стану в стан у момент часу називається величина

.

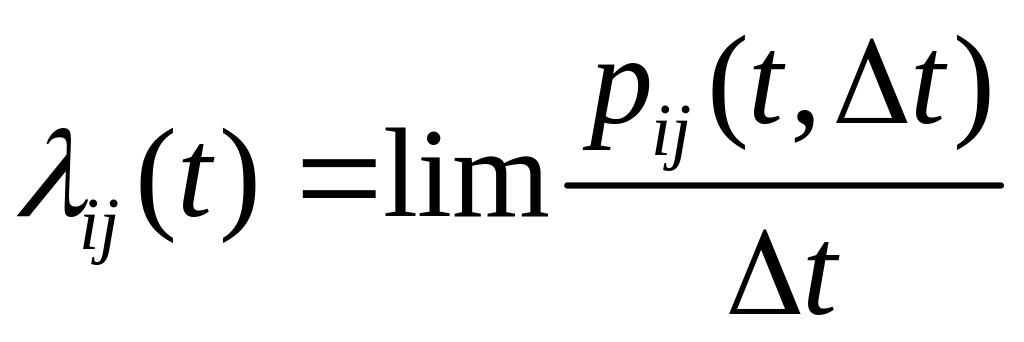З визначення щільності ймовірностей випливає, що

.

З визначення щільності ймовірностей переходу видно, що вона у загальному випадку залежить від часу , невід’ємна та на відміну від імовірності може бути більше 1, але при цьому .

Визначення 8.2. Якщо при будь-якому , щільності ймовірностей переходів не залежать від (тоді замість писатимемо просто , марковський процес з неперервним часом називається однорідним.

Якщо ж хоч би при одній парі значень щільність ймовірностей переходів змінюється з часом , то процес називається неоднорідним.