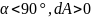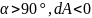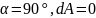Материальная точка – это тело имеющее массу, но размерами которого можно пренебречь в данной задаче.
Тело отсчета – произвольно выбранное нами тело, относительно которого задаются положения всех остальных тел.
Система отсчета – тело отсчета + система координат + часы.
2 способа задания положения тела в пространстве:
Векторный (радиус вектор из т. 0)
Координатный (x,y,z)
Уравнения движения – конкретная зависимость 3 координат от времени(закон движения).
Траектория движения – это некоторая воображаемая нами кривая(линия) которую оставляет за собой тело при своем движении.
Как найти траекторию? Нужно знать уравнение движения, исключить время и связать между собой координаты и нарисовать на графике.
Перемещение – это вектор, соединяющий 2 точки на траектории (Δ
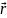 =
2-
1).
=
2-
1).Длина пути – расстояние между 2 точками вдоль траектории(ΔS).
Средняя скорость

Мгновенная скорость
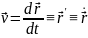 – первая производная от радиус вектора
по времени t.
– первая производная от радиус вектора
по времени t.
Направление
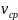 и
и
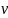 – Направление
– Направление
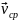 совпадает с
совпадает с
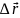 .
.
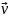 совпадает с направлением касательной
данной точки.
совпадает с направлением касательной
данной точки.Модуль скорости
 .
Производная от длины пути по времени.
.
Производная от длины пути по времени.
2 способа нахождения пути:
Математический.
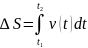
Координатный (графический).
 - площадь фигуры (Геометр. смысл
интеграла).
- площадь фигуры (Геометр. смысл
интеграла).
Среднее ускорение
 .
.
Мгновенное ускорение

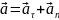
Направление
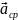 совпадает с
совпадает с
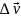 .
.Тангенц ускорение
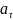 отвечает за изменение вектора скорости
только по величине.
отвечает за изменение вектора скорости
только по величине.
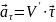 (
(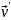 производная от модуля скорости,
производная от модуля скорости,
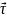 един. вектор в направлении
)
един. вектор в направлении
)
Направление
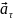 :
:
если
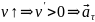 направлен в сторону
направлен в сторону
если
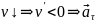 направлен против
направлен против
если
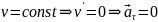
Нормальное ускорение
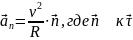 ,
R
радиус кривизны траектории заданной
точки. Отвечает за изменение вектора
скорости только по направлению.
,
R
радиус кривизны траектории заданной
точки. Отвечает за изменение вектора
скорости только по направлению.
Направление
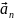 .
Направлено к центру воображаемой
окружности и всегда перпендикулярно
к
.
Направлено к центру воображаемой
окружности и всегда перпендикулярно
к
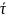
Формулы для
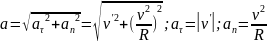
Угловая скорость (
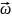 )
)
 –
векторная величина используется для
описания быстроты и направления
вращения. (
–
векторная величина используется для
описания быстроты и направления
вращения. (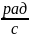 )
)
Направление определяется по правилу буравчика, ручку буравчика вращают в сторону вращения тела, туда куда пойдет острый конец, туда и вектор
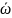 .
всегда перпендикулярен к плоскости
вращения.
.
всегда перпендикулярен к плоскости
вращения.Связь между
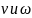 .
.
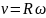
Период вращения Т. Период одного оборота.
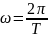
Частота вращения
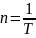 – число оборотов в секунду. (
– число оборотов в секунду. (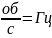 )
)
3 формулы для
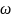 ,
T,
n.
,
T,
n.
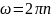
Угловое ускорение.
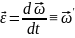
Направление
Если направлен в сторону
Если направлен против
Формулы для
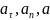 через
вращательные параметры.
через
вращательные параметры.
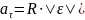
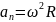
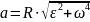
I закон Ньютона: любое тело сохраняет свое состояние покоя или равномерного и прямолинейного движения в отсутствии внешнего воздействия. (1 закон работает не во всех системах отсчета).
ИСО и НИСО: Система где работает I закон, называется ИСО. Система где не работает I закон – НИСО. Дополнительно: Инерциальная система отсчета (ИСО) – либо не подвижна, или движется равномерно и прямолинейно. НИСО – СО движущаяся с ускорением.
II Закон Ньютона:
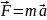 .
Тело массы m
под действием силы
.
Тело массы m
под действием силы
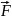 получает ускорение
получает ускорение
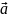 в направлении силы.
в направлении силы. Более общая форма записи II закона:
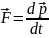

III Закон Ньютона: 2 МТ взаимодействуют друг с другом с силами:
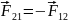 Направлены
противоположно.
Направлены
противоположно.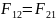 Одинаковые
по величине.
Одинаковые
по величине.Направлены вдоль прямой, соединяющей эти МТ.
Механическая система – совокупность взаимодействующих между собой МТ.
2 вида сил.
Внутренние силы. Они действуют внутри системы. Обозначаются:
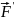
 не производная)
не производная)Внешние силы. Они действуют извне (со стороны тел не входящих в систему).

Закон изменения импульса системы
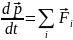 .
Изменение суммарного импульса равно
сумме внешних сил.
.
Изменение суммарного импульса равно
сумме внешних сил.Замкнутая система – если
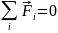 (если сумма внешних сил равна нулю), то
система называется замкнутой, если
нет, то открытой.
(если сумма внешних сил равна нулю), то
система называется замкнутой, если
нет, то открытой.Закон сохранения импульса –
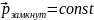 .
Суммарный импульс замкнутой системы
постоянен.
.
Суммарный импульс замкнутой системы
постоянен.Центр масс – это некоторая воображаемая нами точка в пространстве, положение которой определяется радиус вектором
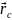 .
Обычно точка С.
.
Обычно точка С.
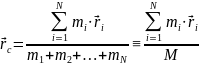 .
.
Скорость и ускорение центра масс
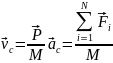 . Если система замкнутая, то ее
. Если система замкнутая, то ее
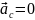 .
Видно, что центр замкнутой системы
движется равномерно, либо прямолинейно.
.
Видно, что центр замкнутой системы
движется равномерно, либо прямолинейно.Малая механическая работа
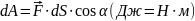 Короткая запись:
Короткая запись:
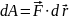
Большая механическая работа
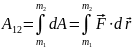 . Работа А12
связана с кинетической энергией МТ:
. Работа А12
связана с кинетической энергией МТ:
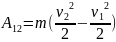
Кинетическая энергия МТ, чистая энергия движения, зависит от скорости:
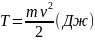
Связь между
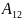 и
и
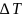 :
:
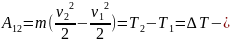 изменение кинетической энергии. Работа
на участке 12, является мерой изменения
кинетической энергии.
изменение кинетической энергии. Работа
на участке 12, является мерой изменения
кинетической энергии.
Консервативная сила – это сила, работа которой не зависит от маршрута движения. Например:
Сила тяжести 2)Гравитационные силы 3)Кулоновские силы между заряженными силами
Диссипативная сила - это сила, работа которой зависит от маршрута движения. Например:
Сила трения
Сила сопротивления среды
Потенциальная энергия – для консервативных сил можно ввести понятие потенциальной энергии тела u, фактически это энергия взаимодействия двух тел, оно зависит от взаимного расположения 2 тел. (Близко или далеко)
Примеры для u
Свободное падение тела расположенного на высоте h над землей. u=mgh
Потенциальная энергия деформирования пружины.
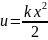 .
k
- жесткость. x
- величина деформации (сжатое или
разжатое).
.
k
- жесткость. x
- величина деформации (сжатое или
разжатое).
Связь между и u.
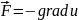
Полная механическая энергия E=T+u, то есть сумма кинетическая + потенциальная.
Закон изменения полной мех. энергии для произв. системы.
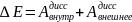
Закон изменения полной мех. энергии для замкнут. системы.
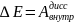 .
.Закон сохранения полной энергии.
Если
диссипативных сил нет, то
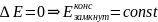
АУУ - это удар когда исходная кинетическая энергия партнеров не затрачивается на их деформацию, и после удара они движутся отдельно.
АНУ – удар, когда исходная энергия партнеров частично затрачивается на их деформацию, и после удара партнеры движутся вместе.
Формулы для u1 и u2
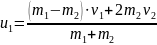
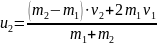
Формула для u при АНУ
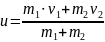
Формулы для и
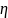 .
.
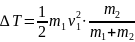
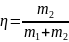
2 примера для η при АНУ:
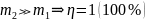 Вся исходная
энергия уходит на деформацию партнеров
(удар молота о наковальню)
Вся исходная
энергия уходит на деформацию партнеров
(удар молота о наковальню)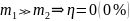 Энергия на
деформацию практически не затрачивается
(забивание гвоздя, молотком).
Энергия на
деформацию практически не затрачивается
(забивание гвоздя, молотком).
Абсолютно твердое тело – это тело не деформирующееся при вращении.
Момент инерции для системы материальных точек -
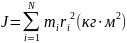
Момент инерции для сплошного твердого тела
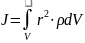 , где
, где
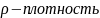
Моменты инерции для 4-х объектов.
Однородный сплошной цилиндр
 :
:
Полый цилиндр:
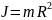
Однородный сплошной шар:
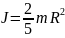
Тонкий стержень. Если ось вращение через середину длины (как буква T)
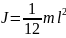 .
Если ось через начало стержня (Г) то
.
Если ось через начало стержня (Г) то
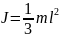 .
.