26 Вопрос Термические коэффициенты

Как и у идеального газа, каждый из основных параметров р, и Т, являясь функцией состояния реального газа, определяется значениями двух других параметров и может быть найден из уравнения

,

которые являются различными формами уравнения состояния.

Таким образом, два любых параметра могут быть приняты за независимые переменные, определяющие значение третьего параметра, а следовательно, и всех других термодинамических величин, являющихся функциями состояния газа.

При этих условиях выше приведенные уравнения состояния в дифференциальной форме будут иметь вид , , ,

где dp,d, dT – полные дифференциалы соответствующих параметров.

В указанные уравнения входят шесть частных производных, которые попарно обратны друг другу, например .

Следовательно, самостоятельное значение из шести частных производных имеют только три. В качестве основных применяются частные производные

,

которые называются термическими коэффициентами. Каждый из термических коэффициентов имеет определенное физическое содержание.

Так, частная производная характеризует интенсивность изменения объема при изменении давления в условиях постоянной температуры. Отношение этой величины к начальному объему газа ₀, взятое с обратным знаком, называется коэффициентом сжатия .

Термический коэффициент характеризует интенсивность увеличения объема при нагревании при постоянном давлении. Отношение этой величины к начальному объему, т.е. , называется коэффициентом объемного расширения.

Наконец, термический коэффициент характеризует интенсивность изменения давления при изохорном нагреве тела. Отношение этой величины к начальному давлению р₀, т.е. , называется коэффициентом упругости.

Названные коэффициенты связаны между собой весьма простым соотношением. Найти это соотношение можно следующим образом. Эта формула позволяет теоретически определить коэффициент упругости, нахождение которого опытным путем затруднительно, в то время как коэффициенты  и  легко определяются экспериментально.

27 вопрос. Уравнение Ван-дер-Ваальса и его анализ

Уравнение состояния реальных газов, в основу которого были поло­жены упрощенные, но правильные по существу представления о молеку-лярно-кинетических свойствах и строении этих газов, было получено в 1873 г. Ван-дер-Ваальсом и носит его имя.

где постоянные а и b зависят от природы газа и у различных газов значи­тельно отличаются друг от друга.

Структура уравнения Ван-дер-Ваальса показывает, что за основу его было взято уравнение состояния идеальных газов рЗ = RT, а затем в него были внесены поправки на объем и давление, которые должны быть приняты во внимание при изучении реальных газов.

Одна поправка учитывает объем, недоступный для движения моле­кул в силу конечности объема самих молекул и наличия взаимодействия между ними. Дело в том, что при беспредельном сжатии газа его объем будет стремиться не к нулю, как у идеальных газов, а к некоторому пре­дельно малому объему b. Величина b больше суммарного объема молекул, т. к. в связи с наличием сил отталкивания, возникающих при их сближе­нии, молекулы газа при сжатии его не могут быть доведены до соприкос­новения. Как было показано в п. 6.1, вокруг каждой молекулы существует как бы сферическая оболочка, в пределы которой не могут проникнуть другие молекулы. Величина b является суммарным объемом таких оболо­чек и составляет примерно учетверенный объем самих молекул. В связи с этим в уравнение состояния следует вводить не полный объем газа, а лишь свободный объем З - b.

Другая поправка учитывает силы взаимного притяжения, действую­щие в направлении действия внешнего давления и как бы увеличивающие его на некоторую добавочную величину, называемую внутренним давле­нием. Полагая, что внутреннее давление газа изменяется пропорционально квадрату плотности или обратно пропорционально квадрату удельного объема газа, Ван-дер-Ваальс принял его равным а/з², где а - коэффициент пропорциональности.

Особенно интересно уравнение Ван-дер-Ваальса тем, что оно качест­венно отображает главную особенность реальных газов - способность пе­реходить при определенных условиях в жидкое состояние. Наглядное представление об этом получается, если преобразовать его в уравнение третьей степени относительно з. Для этого в уравнении (6.20) раскроем скобки в левой части, тогда получаем.

Для выявления физического смысла полученных выводов рассмот­рим в системе координат pu изотермы, построенные по уравнению Ван-дер-Ваальса (рис. 6.5). Первый случай имеет место при высоких тем­пературах, когда изотермы имеют вид кривых гиперболического характера (например, линия 7-2). В этом случае каждому давлению соответствует вполне определенный удельный объем (например, давлению р_а соответст­вует удельный объем З_а). Это значение удельного объема и является дей­ствительным корнем уравнения Ван-дер-Ваальса, оба же мнимых корня в этом случае физического смысла не имеют и должны быть отброшены. Тело в этом случае при любых давлениях находится в газообразном со-

стоянии.

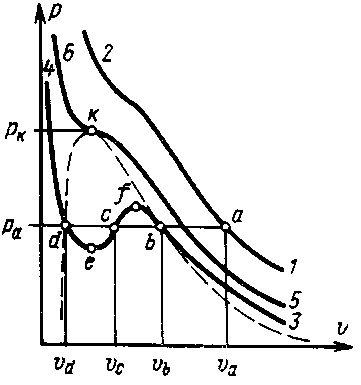
Рис. 6.5

Второй случай имеет место при сравнительно низких температурах, когда изотермы имеют два перегиба (например, линия 3-4).

В этом случае между точками e и f находится область, в которой ка­ждому давлению соответствует три значения удельного объема (например, давлению р_а соответствуют удельные объемы З_ь, З_с и З,Д которые и явля­ются тремя действительными и различными корнями уравнения Ван-дер-Ваальса.

Участок 3-b соответствует изотермическому сжатию тела, находяще­гося в газообразном состоянии, причем в точке b оно уже начинает пере­ходить в жидкое состояние. Точка d соответствует такому состоянию тела, когда оно уже полностью превратилось в жидкость, в соответствии с чем участок d-4 представляет собой изотермическое сжатие жидкости. Точка с соответствует промежуточному двухфазному состоянию тела. Участок кривой b-f соответствует неустойчивому состоянию переохлажденного па­ра, а участок d-e - также неустойчивому состоянию перегретой жидкости. Что касается участка e-f то он вообще физического смысла не имеет, по­скольку в действительности при изотермическом сжатии тело переходит из газообразного в жидкое состояния при постоянном давлении, т. е. по гори­зонтальной линии b-d.

Третий случай имеет место при вполне определенной для каждого тела температуре, когда точки b и d, сближаясь с повышением температу­ры, сливаются в одну точку k, в которой имеет место перегиб соответст­вующей изотермы, причем касательная к ней в этой точке имеет горизон­тальное направление.

Точка k называется критической точкой, а соответствующие ей параметры р_кр, З_кр и Т_кр называются критическими параметрами.

Критическая температура, существование которой было открыто в 1861 г. Д.И. Менделеевым, характеризуется тем, что при температурах выше нее невозможно путем изотермического сжатия добиться перехода газа в жидкое состояние. Критические параметры р_кр и Т_кр обычно определяются эксперимен­тально (определение и_кр опытным путем ненадежно), а по ним можно опреде­лить постоянные а и b в уравнении Ван-дер-Ваальса для данного газа.

Уравнение Ван-дер-Ваальса в безразмерном или, как иногда говорят, в приведенном виде показывает, что если у разных газов два приведенных параметра имеют одинаковое значение, то одинаковым будет и третий па­раметр. Например, если приведенные давления и температуры двух разных газов равны, то равны и их приведенные удельные объемы.

Состояния разных газов, при которых их приведенные параметры п—,т равны, называются соответственными состояниями. Следовательно,

если два приведенных параметра у разных газов равны, то эти газы нахо­дятся в соответственных состояниях. Это положение, представляющее со­бой общую закономерность в изменении состояния реальных газов (в предположении, что они подчиняются уравнению Ван-дер-Ваальса), но­сит название закона соответственных состояний.

Реальные газы, находящиеся в соответственных состояниях, являют­ся термодинамически подобными. Это означает, что при одинаковых п—,т свойства всех газов в отношении давления, удельного объема

и температуры идентичны. Иными словами, если из данных эксперимента известны свойства какого-либо реального газа, то по ним без всякого экс­перимента можно определить аналогичные свойства любого другого газа, находящегося с ним в соответственном состоянии.