- •Российская федерация министерство образования и науки
- •Билет № 1
- •Для графа, заданного симметричной матрицей расстояний:
- •Доказать тождество, используя только определения операций над множествами:
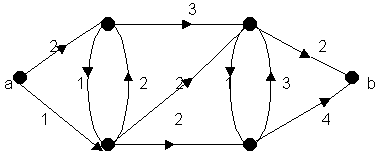
- •Следующие данные определяют ориентированный граф, пропускные способности дуг и заданный на графе поток:
- •Доказать тождество, используя только определения операций над множествами: .
- •Граф задан матрицей весов. Построить дерево кратчайших расстояний из 1 вершины.
- •Граф задан матрицей весов. Построить матрицу кратчайших расстояний.
- •Граф задан матрицей весов. Построить минимальный остов.
- •Граф задан матрицей весов. Построить минимальный остов.
- •Зав. Кафедрой по Захарова и.Г.
- •Граф задан матрицей весов. Построить дерево кратчайших расстояний из 1 вершины.
- •Граф задан матрицей весов. Построить дерево кратчайших расстояний из 1 вершины.
- •Для графа, заданного матрицей весов построить дерево кратчайших расстояний:
- •Доказать тождество, используя только определения операций над множествами:
- •Для графа, заданного матрицей весов построить минимальный остов:
- •Доказать тождество, используя только определения операций над множествами:
- •Для графа, заданного матрицей весов, построить матрицу кратчайших расстояний:
- •Для графа, заданного матрицей весов, построить минимальный остов:
- •Доказать тождество, используя только определения операций над множествами: .
- •Для графа, заданного матрицей весов построить матрицу кратчайших расстояний:
- •Для графа, заданного матрицей весов построить дерево кратчайших расстояний:
- •Зав. Кафедрой по Захарова и.Г.
- •Для графа, заданного матрицей весов построить минимальный остов:
- •Для графа, заданного матрицей весов построить дерево кратчайших расстояний:
- •Зав. Кафедрой по Захарова и.Г.
- •Для графа, заданного матрицей весов построить матрицу кратчайших расстояний:
- •Для графа, заданного матрицей весов построить минимальный остов:
- •Зав. Кафедрой по Захарова и.Г.
- •Для графа, заданного матрицей весов построить матрицу кратчайших расстояний:
- •Для графа, заданного матрицей весов построить дерево кратчайших расстояний:
- •Доказать тождество, используя только определения операций над множествами:
- •Для графа, заданного матрицей весов построить минимальный остов:
- •Доказать тождество, используя только определения операций над множествами: .
- •Для графа, заданного матрицей весов построить дерево кратчайших расстояний:
- •Для графа, заданного матрицей весов построить матрицу кратчайших расстояний:
- •Для графа, заданного матрицей весов построить минимальный остов
- •Для графа, заданного матрицей весов построить минимальный остов
- •Доказать тождество, используя только определения операций над множествами:
- •Для графа, заданного матрицей весов построить минимальный остов
- •Доказать тождество, используя только определения операций над множествами:
- •Доказать тождество, используя только определения операций над множествами:
- •Доказать тождество, используя только определения операций над множествами: .
- •Доказать тождество, используя только определения операций над множествами:
- •Для графа, заданного матрицей весов построить дерево кратчайших расстояний:
- •Для графа, заданного матрицей весов построить минимальный остов:
- •Следующие данные определяют ориентированный граф, пропускные способности дуг и заданный на графе поток:
Чему равна сумма
 ?
?Для графа, заданного матрицей весов построить минимальный остов
6
5
7
5
6
6
9
8
3
7
8
5
9
4
6
7
1
8
7
8
4
2
7
4
3
3
6
2
4
3
2
5
7
7
7
4
9
8
1
4
3
9
5
6
8
3
2
5
Доказать тождество, используя только определения операций над множествами:
В комнате студенческого общежития живут трое студентов. У них есть 4 чашки, 5 блюдец и 6 чайных ложек (все чашки, блюдца и ложки отличаются друг от друга). Сколькими способами они могут накрыть стол для чаепития (каждый получает 1 чашку, 1 блюдце и 1 ложку)?
Зав.
кафедрой ПО
Захарова И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 28
Сколько беспорядков существует на пяти символах? На четырех символах?
Для графа, заданного матрицей весов построить минимальный остов
6
5
9
4
2
5
6
5
8
6
9
4
2
6
5
4
6
9
2
1
6
4
9
5
4
5
5
4
3
3
1
8
6
5
4
3
2
4
1
4
6
9
5
4
2
6
3
1
2
9
2
4
3
2
4
6
4
4
1
3
2
6
4
9
9
5
2
6
3
4
3
6
9
6
6
4
1
1
1
4
9
6
Упростить выражение .
Сколькими способами можно выбрать из полной колоды, содержащей 52 карты, 6 карт так, чтобы среди них были все 4 масти?
Зав.
кафедрой ПО
Захарова И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 29
Основные свойства матриц бинарных отношений.
Из основных законов алгебры множеств получите следующий результат:
Человек имеет 6 друзей и в течение 20 дней приглашает к себе по 3 человека так, что компания ни разу не повторяется. Сколькими способами может он это сделать?
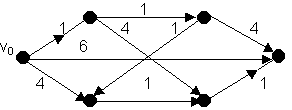
Используя алгоритм Дейкстры, найти расстояния от вершины v0 до остальных вершин сети:
Зав.
кафедрой ПО
Захарова И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 30
Студенту надо выбрать два факультативных курса из шести предлагаемых. Сколько имеется способов для выбора если чтение двух курсов начинается в 10 часов, чтение двух других в 12 часов, а в остальном курсы не пересекаются по времени?
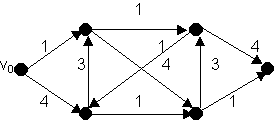
Используя алгоритм Дейкстры, найти расстояния от вершины v0 до остальных вершин сети:
Упростить выражение: .
При каких n существуют графы с n вершинами, каждая из которых имеет степень 3? Степень 4?
Зав.
кафедрой ПО
Захарова И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 31
Доказать, что
Хор состоит из 10 участников. Сколькими способами можно в течение 3 дней выбирать по 6 участников, так, чтобы каждый день были разные составы хора?
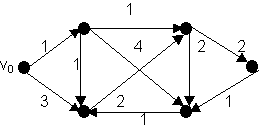
Используя алгоритм Дейкстры, найти расстояния от вершины v0 до остальных вершин сети:
Какое наименьшее число рёбер может быть в связном графе с n вершинами? Почему?
Зав.
кафедрой ПО
Захарова И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 32
Из основных законов алгебры множеств получите следующие результаты:
Сколько различных четырёхзначных чисел можно составить из цифр 0,1,2,3,4,5,6, если каждая из них может повторяться несколько раз?
Найти все минимальные разрезы сети:
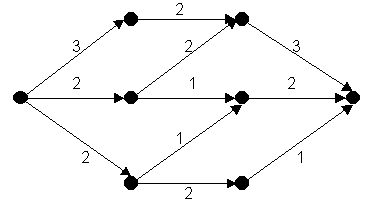
Сколько рёбер в связном графе с n вершинами, если в нём имеется единственный цикл? Почему?
Зав.
кафедрой ПО
Захарова И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 33
Сеть. Поток в сети. Задача о максимальном потоке в сети. Разрез.
Упростить выражение: .
Сколькими способами можно расставить 12 белых и 12 чёрных шашек на чёрных полях шахматной доски?
Найти все минимальные разрезы сети:
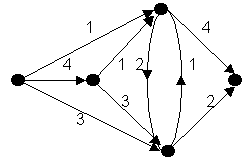
Зав.
кафедрой ПО
Захарова И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 34
Сколько неотрицательных целых чисел, меньше, чем миллион, содержат все цифры 1,2,3,4? Сколько чисел состоит только из этих цифр?
Найти все минимальные разрезы сети:

Приведите пример двух различных транзитивных отношений на множестве .
Упростить выражение .
Зав.
кафедрой ПО
Захарова И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 35
Из 12 слов мужского рода, 9 женского и 10 среднего надо выбрать по 1 слову каждого рода. Сколькими способами может быть сделан этот выбор?
Найти все минимальные разрезы сети: