Российская федерация министерство образования и науки
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
Билет № 1
n-местное отношение. Бинарное отношение. Способы задания бинарного отношения на конечном множестве. Виды бинарных отношений.
Доказать тождество, используя только определения операций над множествами:
В оранжерее имеются цветы десяти наименований. Сколькими способами можно составить букет из 20 цветов?
Для графа, заданного симметричной матрицей расстояний:
6 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
0 |
4 |
3 |
1 |
|
|
|
1 |
4 |
0 |
2 |
|
2 |
4 |
|
2 |
3 |
2 |
0 |
1 |
4 |
|
|
3 |
1 |
|
1 |
0 |
1 |
7 |
|
4 |
|
2 |
4 |
1 |
0 |
|
4 |
5 |
|
4 |
|
7 |
|
0 |
1 |
6 |
|
|
|
|
4 |
1 |
0 |
проверить,
будет ли дерево
деревом кратчайших расстояний.
Зав.
кафедрой ПО
Захарова
И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 2
Доказать тождество, используя только определения операций над множествами:
Из группы, состоящей из 7 мужчин и 4 женщин, нужно выбрать 6 человек так, чтобы среди них было не менее двух женщин. Сколькими способами это можно сделать?
Следующие данные определяют ориентированный граф, пропускные способности дуг и заданный на графе поток:
Дуги графа |
(s,1) |
(s,5) |
(1,4) |
(1,2) |
(2,3) |
(4,3) |
(5,2) |
(3,t) |
Пропускные способности дуг |
2 |
2 |
2 |
2 |
2 |
1 |
2 |
4 |
Поток на дугах |
2 |
0 |
0 |
2 |
2 |
0 |
0 |
2 |
Максимальный ли это поток? Нельзя ли его улучшить? Если да, то сделать это, получив максимальный поток.
Дан полный граф на 8 вершинах. Сколько рёбер необходимо удалить, чтобы он стал деревом? Почему?
Зав.
кафедрой ПО
Захарова
И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 3
Упростить выражение
.Сколькими способами можно разложить 10 книг на 5 бандеролей по 2 книги в каждой (порядок бандеролей не принимаем во внимание)?
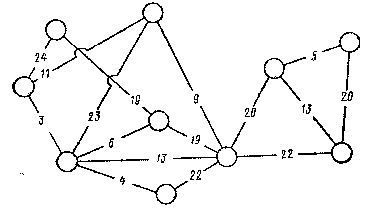
Для графа, изображённого на рисунке, построить минимальный покрывающий остов.
Приведите пример двух различных рефлексивных отношений на множестве
Зав.
кафедрой ПО
Захарова
И.Г.
РОССИЙСКАЯ ФЕДЕРАЦИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики, естественных наук и информационных технологий
Кафедра программного обеспечения
Дисциплина Дискретная математика Курс 1
Специальность Информационная безопасность Семестр 1
БИЛЕТ № 4