34

Цифровая обработка сигналов

Основные положения теории

аналоговых и цифровых сигналов

1 Спектральный метод

1.1 Собственные функции оператора динамической системы

В динамической системе, имеющей один вход и один выход, связь входного u(t) и выходного v(t) сигналов описывается с помощью оператора L (рисунок 1.1)

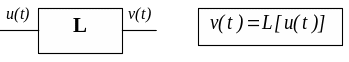
Рисунок 1.1

При построении математических моделей динамических систем важную роль играет понятие о собственных функциях (собственных сигналах) оператора L. Определением собственной функции оператора L служит следующее равенство

,

из которого следует, что собственный сигнал при прохождении через динамическую систему не изменяет свою форму. Чтобы определить реакцию системы на собственный сигнал, достаточно определить постоянный коэффициент , который называют собственным числом. Таким образом, при сохранении формы сигнала соотношение между входом и выходом определяется константой (коэффициентом передачи).

В различных областях техники, включая обработку сигналов, часто приходится иметь дело с динамическими системами, описываемыми обыкновенными дифференциальными уравнениями с постоянными коэффициентами

.

Базовым для таких систем является оператор дифференцирования

.

Собственной функцией дифференциального оператора является экспонента

,

а собственным числом – коэффициент при показателе экспоненты p. Обозначив оператор дифференцирования через p, можем записать дифференциальное уравнение системы в следующем виде

.

Важную роль при анализе таких систем имеют синусоидальные сигналы. Синусоидальный сигнал с фиксированной частотой и с произвольными амплитудой и фазой можно рассматривать как действительную часть экспоненциального сигнала

.

Из данного выражения следует, что полную информацию о синусоидальном сигнале дает комплексная амплитуда

,

.

Синусоидальный сигнал (функция времени) и комплексная амплитуда (комплексное число) изоморфны, т.е. по сигналу можно определить комплексную амплитуду и обратно по комплексной амплитуде можно построить синусоидальный сигнал

.

Таким образом, синусоидальный сигнал можно изображать точкой на комплексной плоскости. Связь амплитуды и фазы с действительной и мнимой частями комплексной амплитуды определяется простыми геометрическими соотношениями (рисунок 1.2).

Рисунок 1.2

При дифференцировании произвольного синусоидального сигнала получим следующее

.

Поставим вопрос, что происходит с комплексной амплитудой синусоидального сигнала при его дифференцировании? Выполнив соответствующие преобразования, получим

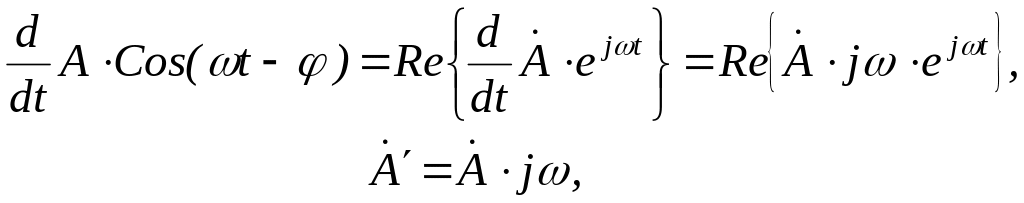
т.е. при дифференцировании синусоидального сигнала его комплексная амплитуда умножается на j. Умножение на  означает изменение амплитуды и размерности сигнала , а умножение на j соответствует сдвигу фазы на /2. Действительно, легко убедиться, что сигнал с комплексной амплитудой равен производной исходного сигнала

.

Представление синусоидального сигнала (функции времени) комплексной амплитудой (числом) составляет основу символического метода, используемого в электротехнических расчетах цепей переменного тока. Его использование позволяет свести задачу расчетов электрических цепей при синусоидальных входных сигналах в установившемся режиме к сравнительно простой алгебраической задаче.

1.2 Емкости, индуктивности, активные сопротивления. Цепи переменного тока

Конденсаторы, резисторы и катушки индуктивности являются основными элементами электрических, электронных и радиотехнических цепей. Связь между мгновенными значениями токов и напряжений для емкостей и индуктивностей устанавливается с помощью дифференциального оператора (рисунок 1.3)

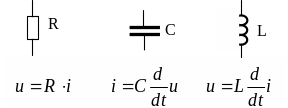
Рисунок 1.3

Если рассматривать установившийся режим в цепи при синусоидальных токах и напряжениях, то целесообразно в качестве коэффициентов, характеризующего одновременно амплитуду и фазу синусоиды, принять комплексные амплитуды токов и напряжений

,

.

В этом случае связи между мгновенными значениями токов и напряжений в элементах цепи соответствуют определенные соотношения между комплексными амплитудами токов и напряжений

.

Эти соотношения позволяют определить комплексные сопротивления переменному току для элементов цепи

,

с помощью которых можно перенести все методы расчета цепей постоянного тока на цепи переменного тока. Иногда удобнее множитель , появляющийся при дифференцировании синусоиды, обозначать одной буквой p и называть этом множитель оператором дифференцирования.

Если рассматривать четырехполюсник, содержащий любое число сопротивлений, емкостей и индуктивностей произвольной конфигурации (рисунок 1.4), то его математической моделью будет дифференциальное уравнение с постоянными коэффициентами.

Рисунок 1.4

Если принять, что входной и выходной сигналы соответственно равны и , то после подстановки этих сигналов в дифференциальное уравнение получим алгебраическое уравнение, связывающее комплексные амплитуды напряжений на входе и выходе цепи

.

Это уравнение позволяет определить передаточную функцию цепи как отношение комплексной амплитуды на выходе к комплексной амплитуде на входе

.

Таким образом, передаточную функцию цепи можно определить по коэффициентам дифференциального уравнения.

Передаточная функция устанавливает связь комплексных амплитуд входного и выходного сигналов

.

Комплексные амплитуды позволяют получить и аналитические выражения входного и выходного сигналов как функций времени

Соотношение амплитуд входного и выходного сигналов определяется модулем передаточной функции для данной частоты, а сдвиг фазы выходного сигнала определяется аргументом передаточной функции

В соответствие с этим зависимость модуля передаточной функции от частоты называют аплитудно-частотной характеристикой цепи (АЧХ), а зависимость аргумента передаточной функции от частоты – фазо-частотной характеристикой (ФЧХ).

1.3 Два простых примера расчета передаточной функции цепей

Интегрирующая цепочка

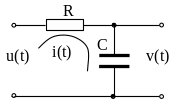
Рисунок 1.5

Используя соотношения для мгновенных значений токов и напряжений на конденсаторе и резисторе, получим дифференциальное уравнение для данной цепи

При синусоидальных входных сигналах дифференциальное уравнение для мгновенных значений входного и выходного напряжений трансформируется в алгебраическое уравнение для комплексных амплитуд входного и выходного сигналов

,

откуда получим выражение передаточной функции цепи

.

На рисунке 1.6 показаны АЧХ и ФЧХ данной цепи при постоянной времени =10 мс. Интегрирующая цепочка является фактически простейшим фильтром нижних частот. Граничная частота полосы пропускания по уровню 0.7 равна f_c=1/2. Цепь на этой частоте сдвигает фазу входного сигнала на -45.

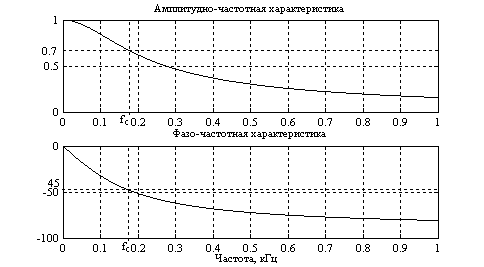
Рисунок 1.6

Более сложная цепь с двумя реактивными элементами показана на рисунке 1.7. Ее называют мостом Вина.

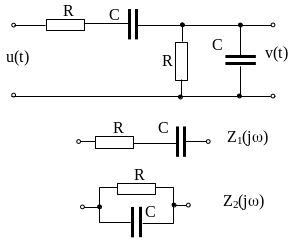
Рисунок 1.7

Эту цепь можно рассматривать как делитель напряжения на двух комплексных сопротивлениях Z₁(j) и Z₂(j). При этом передаточную функцию цепи можно записать в следующем виде

.

Рассчитаем сопротивления Z₁(j) и Z₂(j)

,

.

Следовательно, передаточная функция цепи равна

.

На рисунке 1.8 показаны АЧХ и ФЧХ этой цепи. Из графиков видно, что мост Вина является низкодобротной резонансной цепью. Резонансная частота равна f₀=2/. В точке резонанса коэффициент передачи |W(j)|=1/3, фазовый сдвиг равен 0.

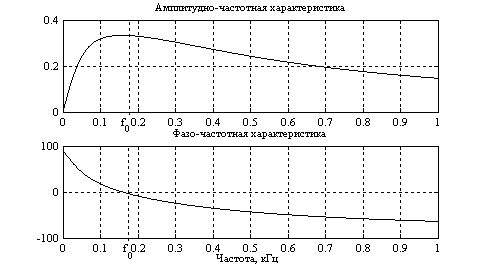
Рисунок 1.8