1.3. Виртуальный эксперимент
Как правило, под виртуальным экспериментом понимается имитационный эксперимент.
Замена реального объекта на алгоритм моделирующий его поведение при воспроизведении реакции окружающей среды называется имитационным экспериментом.
Обычно вычисление, производимое с помощью аналитической модели в традиционной вычислительной процедуре дает одно вычисляемое значение – показатель эффективности.
При имитационном эксперименте поведение модели изучается под влиянием входных воздействий, часть из которых носит случайный характер. В результате такого наблюдения получается набор экспериментальных данных, на основе которых оцениваются характеристики системы.
В основе статистического эксперимента лежит метод Монте-Карло, состоящий в том, что результат испытания зависит от значений случайной величины, распределенной по заданному закону. Теоретической основой метода Монте-Карло является предельные теоремы теории вероятностей (т. Чебышева, т. Бернулли, т. Пуассона).
Описание поведения системы
Описание поведения системы – основа любой имитационной системы. Концепция модели строится на 3-х шагах:
определение принадлежности системы к одному из известных классов;
описание рабочей нагрузки;
выбор уровня детализации представления системы в модели;
Все последующие действия по созданию модели относятся к ее формализации, которая предполагает следующие шаги:
выбор метода представления динамики системы.
формальное математическое описание случайных факторов, подлежащих учету в модели.
выбор механизма изменения масштаба модельного времени.
Управление модельным временем
Скорость протекания большинства реальных процессов значительно ниже скорости реализации модельного эксперимента.
В связи с эти м приходится соотносить три представления времени:
1.Реальное время, в котором функционирует система.
2.Модельное время, в котором организуется работа модели.
3.Машинное время, отражающее затраты вычислительных ресурсов на проведение имитаций.
Выбор метода управления модельным временем (с постоянным шагом и по особым состояниям) зависит от назначения модели, ее сложности и требуемой точности.
Изменение времени с постоянным шагом
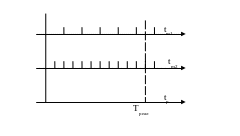
Если события в модели появляются регулярно, их распространение во времени равномерно, число событий велико, а моменты их появления близки, то целесообразно использовать метод постоянного шага.
Результат моделирования напрямую зависит от величины выбранного шага. Обычно выбирают шаг, равный среднему интервалу между наиболее частыми и наиболее важными событиями.
Измерение времени по особым состояниям
В этом случае системное время каждый раз изменяется на величину, строго соответствующую интервалам времени до момента очередного наступления события.
Для реализации моделирования по особым состояниям требуется планирование событий или разработка календаря. Календарь может быть задан в виде закона распространения интервалов между событиями или моменты наступления событий могут задаваться некоторым логическим условием, которое проверяется на каждом шаге моделирования.
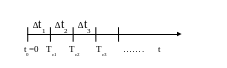
Моделирование по особым состояниям целесообразно, если:
События распространяются во времени неравномерно или интервалы между ними велики.
Предъявляется повышение требования в точности определения взаимного расположения.
Необходимо учитывать наличие одновременных событий
Компоненты реальных систем могут характеризоваться величинами, которые измеряются в разных единицах времени. В этом случае они должны быть предварительно переведены к этому масштабу.