7. Розрахунок систем двигуна

8.1 Система мащення, радіальний підшипник ковзання

Вибір мастила для підшипника ковзання

Перш за все, необхідно здійснити вибір мастила відповідно до умов роботи двигуна. Динамічна в’язкість мастила, як було встановлено раніше, є одним з головних параметрів, які визначають вантажність підшипника ковзання.

Моторні мастила, які використовують для поршневих двигунів внутрішнього згоряння, є найбільш вживаними в практиці експлуатації машин різного призначення.

У міжнародному масштабі прийнято для класифікації мастил систему . (Society of Automotive Engineers – Товариство автоінженерів). При цьому моторні мастила ділять на шість зимових ( ) і п’ять літніх ( ); буква „ ” (Winter – зима). Існують також всесезонні мастила, номери яких позначають як комбінацію зимових і літніх номерів. Наприклад, і т. ін.

На рисунку 8.1 наведено рекомендації з підбору мастила у залежності від температурного режиму (шкала зверху) їх використання.

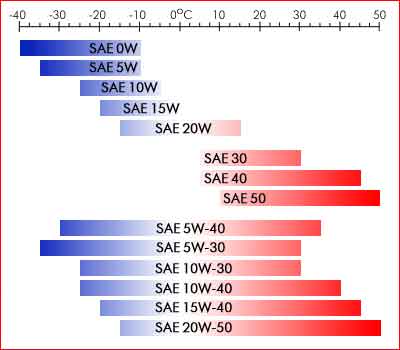
Рисунок 8.1 – Рекомендації SAE для вибору мастила у залежності від температурного режиму роботи двигуна

Також широко використовуються моторні мастила, які виготовляють у країнах СНД, відповідно до ГОСТ 8581-78. Марки указаних мастил наступні: М-10В₂, М-8Г₂, М-10Г₂, М-8Г₂к, М-10Г₂к, М-8ДМ, М-10ДМ і ін. ( Всі М-10 – літні мастила; М-8 – зимові).

В’язкість мастила є головною його характеристкою. Вона характеризує внутрішнє тертя мастила при його течії (протидія двох суміжних шарів рідини при їх ламінарному зміщенні); при зростанні температури в’язкість зменшується, при зниженні – зростає.

Коефіцієнт рідинного тертя становить 0,003 – 0,03, що в 50 –100 разів менше, ніж при терті без мащення (0,08 –0,15).

В’язкість класифікують як динамічну (у системі СІ – Па∙с, або mПа∙с – міліпаскаль∙секунда; П (пуаз), сП (сантіпуаз) – технічна система одиниць) і кінематичну (м²/с, мм²/с (Ст (стокс) – система СІ), Ст=0,1 Па∙с, сСт (сантистокс) – технічна система одиниць). У ньютоновських рідинах напруження зсуву пропорційно швидкості зсуву. Коефіцієнт пропорційності при цьому – є динамічна в’язкість.

У довідниках приводяться максимальна і мінімальна кінематичні в’язкості мастила при 100⁰С, а також мінімальна динамічна в’язкість при 150⁰С і швидкості зсуву 10⁶с^-1.

Якщо величину кінематичної в’язкості помножити на показник густини мастила при температурі заміру, то отримаємо динамічну в’язкість мастила.

Індекс в’язкості (ІВ) – параметр для визначення в’язкості при різних температурах: чим вище його числове значення, тим менше змінюється в’язкість при різних температурах мастил. Однодіапазонні мастила мають ІВ біля 100, багатодіапазонні – до 150.

Згідно з специфікацією в’язкість мастил вибирається відповідно до умов їх експлуатації.

Літнє мастило має достатню в’язкість для забезпечення надійного змащування при високій температурі, проте воно надто густе при низькій температурі, що веде до ускладнень при запуску двигуна взимку.

Зимове мастило з низькою в’язкістю забезпечує холодний запуск двигуна при низькій температурі, однак не забезпечує його надійного мащення влітку, коли температура мастила при роботі двигуна може сягати 100⁰С і більше. Саме з указаних міркувань найбільш широке розповсюдження отримали всесезонні мастила, які мають найменшу залежність в’язкості від температури.

Для оцінки в’язкості мастил також використовують такі характеристики, як в’язкість мастила при прокручуванні стартером двигуна при низькій температурі і прокачуванні мастила насосом по системі мащення при холодному запуску. Останні характеристики (динамічна в’язкість) вказують лише для зимових або всесезонних мастил і для ряду значень від’ємних температур.

У таблиці 8.1 наведено характеристики в’язкості мастил згідно з класифікацією SAE.

Таблиця – 8.1 Класифікація в’язкості мастила згідно з даними SAE

Клас пoSAE	Низькотемпературна в’язкість		Високотемпературна в’язкість
	Прокручування	Прокачування	В’язкість, мм2/с, при 100° С		В’язкість, МПа • с, при 150 °С і швидкості зсуву 106с-1, нe менше
	Максимальна в’язкість, МПа • с, при t,°С	Максимальна в’язкість, МПа • с, при t,°С	Min	Max
0W	3250 при -30°С	60000 при -40°С	3,8	-
5W	3500 при -25°С	60000 при -35°С
10W	3500 при -20°С	60000 при -30°С	4,1	-	-
15W	3500 при -15°С	60000 при -25°С	5,6	-	-
20W	4500 при -10°С	60000 при -20°С	5,6	-	-
25W	3250 при -5°С	60000 при -15°С	9,3	-	-
20	-	-	5,6	<9,3	2,6
30	-	-	9,3	<12,5	2,9
40	-	-	12,5	<16,3	2,9
40	-	-	12,5	<16,3	3,7
50	-	-	16,3	<21,9	3,7
60	-	-	21,9	<26,1	3,7

У таблиці 8.2 наведено відповідність в’язкостей моторних мастил згідно з ГОСТ 17479.1- 85 (країни СНД) і класифікацією SAE

Літерою „з” позначено зимові мастила, а дріб (наприклад, 5з/14) – всесезонне мастило. Якщо взяти мастило М-10Г₂ (ГОСТ 8581-78), де літерою „М” позначено приналежність до моторних мастил, цифрою 10 – клас в’язкості (кінематична в’язкість при 100⁰С 9,3–11,5 мм²/с(сСт)), літерою „Г” з індексом 2 – призначення мастила для високофорсованих дизелів, то йому відповідає мастило SAE .

_{Таблиця 8.2 – Відповідність в’язкостей моторних мастил згідно з ГОСТ 17479.1-85 і класифікацією SAE}

Клас в’язкості		Клас в’язкості
ГОСТ17479-85	SAE J 300	ГОСТ17479-85	SAE J 300
1	2	3	4
3з	5W	24	60
1	2	3	4
4з	10W	3з/8	5W-20
5з	15W	4з/6	10W-20
6з	20W	4з/8
1	2	3	4
6	20	4з/10	10W-30
8		5з/10	15W-30
10	30	5з/12
12		5з/14	15W-40
14	40	6з/12	20W-30
16		6з/14	20W-40

На рисунку 8.2 наведено графіки залежності динамічної в’язкості від температури для ряду сортів моторних мастил.

Рисунок 8.2 – Залежність динамічної в’язкості мастил від температури

На рисунку 8.2: 1 – МК-22; 2 – МС-20; 3 – АК-15; 4 – ДП-14; 5 – ДП-11;

6 – АК-10; 7 – ДП-8; 8 – АК-6 і АС-5; 9 – АКЗп-6

Наприклад, із графіка 8.2 для мастила ДП-14 (дизельне мастило, яке широко використовувалось у автомобільних і тракторних двигунах, з кінематичною в’язікстю 14 сСт) при температурі знаходимо Па∙с.

У системі МКГСС одиницею динамічного коефіцієнта в’язкості являється кГ·с/м², а в системі СІ – Па·с. Зв’язок між названими одиницями наступний: 1 Пуаз=0.010193 кГ·с/м² = 0,1 Па·с; 1 кГ·с/м² =98,1 Пуаз = 9,81Па·с.

Одиницею кінематичного коефіцієнта в’язкості у системі СГС є стокс (Ст). 1Ст = 1см²/с; у системі МКГСС і СІ – 1 м²/с = 10⁴ Ст.

Зв’язок між кінематичною і динамічною в’язкістю виражається залежністю:

(8.1)

де ν – коефіцієнт кінематичної в’язкості, м²/с;

ρ – густина мастила, кг/м³.

При зростанні температури, в’язкість мастила знижується. Вплив температури на коефіцієнт динамічної в’язкості оцінюється формулою:

μ = μ₀·e^{(t - t0 )}, (8.2)

де μ, μ₀ – відповідно значення коефіцієнта динамічної в’язкості при температурах t і t₀ градусів;

а - показник степені; для автотракторних мастил а = 0,025…0,035.

Для визначення кінематичної в’язкості автотракторних мастил також може бути використано формулу:

ν_t=ν₅₀·(50/t)ⁿ, (8.3)

де  ν_t – коефіцієнт кінематичної в’язкості при температурі t; ν₅₀ – коефіцієнт кінематичної в’язкості при температурі   50 ⁰С; 

t - температура, при якій потрібно визначити в’язкість, ⁰С;

n – показник степені, який змінюється у межах від 1,8 до 2,6.

Значення  n залежно від в’язкості ν  при 50 ⁰С наведено в таблиці 8.3.

Таблиця 8.3 – Залежність показника степені n від кінематичної в’язкості мастила

ν50, сСт	12	21	29	37	45	53	60	68	80
n	1,8	2,0	2,1	2,2	2,3	2,4	2,5	2,52	2,56

Показник n може також визначатись з наступного виразу:

n = lgν₅₀+2,7. (8.4)

Розрахунок радіального підшипника ковзання

Розрахунок радіальних підшипників ковзання у автотракторному машинобудуванні традиційно ведуть по середньому тиску К, який створюється зовнішнім навантаженням Р на площу проекції вкладиша підшипника:

(8.5)

де – довжина опірної поверхні шийки вала, м;

– діаметр шийки вала, м.

Середні і максимальні значення тиску на радіальні підшипники ковзання автотракторних двигунів наведено в таблиці 8.4.

Таблиця 8.4 – Значення тиску на радіальні підшипники ковзання автотракторних двигунів

Тип двигуна і автомобіля	Підшипники	Кср, МПа	Кmax, МПа
Бензинові для легкових автомобілів	Шатунні Корінні	6…8 5…7	8…10 6…8
Бензинові для вантажних автомобілів	Шатунні Корінні	5…7 4…6	7…10 5…7
Дизелі для автотракторних двигунів	Шатунні Корінні	4…5 5…6	8…12 7…9
Форсовані двигуни внутрішнього згоряння	Шатунні Корінні	9…16 10…17	25…35 20…30

Міждержавним Європейським стандартом МЄСТ ІСО 7902 – 1 2001 „Гідродинамічні радіальні підшипники ковзання, які працюють у стаціонарному режимі. Круглоциліндричні підшипники. Метод розрахунку”, регламентуються наступні характеристики і параметри: число Рейнольдса, при якому забезпечується ламінарний потік мастила в підшипнику; параметр Зоммерфельда, яким характеризується несуча здатність підшипника; витрати мастила через підшипник; втрати потужності на тертя; параметри теплового балансу.

Число Рейнольдса визначається за формулою:

(8.6)

де – число Рейнольдса;

– номінальний внутрішній діаметр підшипника, м;

– ефективний діаметральний зазор у підшипнику;

– відносний зазор у спряженні підшипник-вал;

– кутова швидкість обертання колінчастого вала, с^-1.

Для двигуна СМД-14 = π·n/30 = π·1700/30 = 178с^-1;

– динамічна в’язкість мастила при робочій температурі підшипника, Па·с.

Для робочої температури (90 ⁰С) і мастила ДП-14 з графіка на рисунку 9.2 знаходимо Па·с;

– густина мастила. Для автотракторних двигунів = 900…920 кг/м³. Приймаємо для розрахунків = 900 кг/м³.

Робочий зазор у підшипнику залежить від посадки і теплового розширення вала і підшипника. При нормальних умовах ( ) відносний зазор у підшипнику визначають за формулами:

(8.7) де , , – відповідно максимальний, мінімальний і середній відносні зазори в підшипнику;

– відповідно максимальний, мінімальний і номінальний діаметри підшипника, а також – максимальний і мінімальний діаметри вала.

Зміна зазору із-за теплового розширення вала і підшипника визначається за формулою:

(8.8)

де , – коефіцієнти лінійного розширення підшипника і вала відповідно. Приймаємо = 23·10^-6 град^-1; = 11·10^-6 град^-1;

, – температура підшипника і вала відповідно. Приймемо для розрахунку , = 90 ⁰С. = 40 ⁰С – температура оточуючого середовища.

Отже, м.

Для корінного підшипника колінчастого вала двигуна СМД-14 максимальні і мінімальні значення діаметрів підшипника і вала, а також номінальний діаметр спряження відповідно =88,045·10^-3м;

= 88,0040·10^-3м; = 87,900·10^-3м; = 87,885 ·10^-3м; =88·10^-3м.

Після підстановки розмірів діаметрів, знаходимо максимальне, мінімальне і середнє значення відносного діаметру:

= 0,00182; = 0,00118; = 0,0015.

З урахуванням теплових змін розмірів вала і підшипника, відносний зазор у спряженні підшипник-вал має значення:

Підставляючи значення розрахункових параметрів, знаходимо число Рейнольдса:

= 240,7 < 901,2.

Отже, потік мастила в підшипнику ламінарний.

Визначаємо навантаження, які передаються на шип вала у підшипнику ковзання. У двигуні вони створюються силами тиску робочого тіла у циліндрі і силами інерції рухомих мас кривошипно-шатунного механізму. Максимального значення навантаження сягають, коли поршень знаходиться поблизу верхньої мертвої точки (в.м.т), під час самозаймання палива або запалювання робочої суміші. При цьому на поршень діє сила:

(8.9)

де – сила, що діє на поршень при самозайманні палива в циліндрі двигуна; – тиск газів на дно поршня; для тракторних дизелів при розрахунках рекомендується приймати ;

– площа поверхні дна поршня; – сила інерції поршневої групи:

(8.10)

– маса деталей поршневої групи, що рухаються зворотно-поступально (дорівнює сумі мас поршневого комплекту (поршень, палець, поршневі кільця) і частини маси шатуна, віднесеної до поршня); для двигуна СМД-14 кг; – радіус кривошипа колінчастого вала; м_{; ширина корінного підшипника колінчастого вала} = 0,08 м; діаметр корінної шийки вала м;

– кутова швидкість обертання колінчастого вала, с^-1; ; для двигуна СМД-14

Знаходимо силу інерції поршневої групи, враховуючи, що при положенні поршня в в.м.т., вона має максимальне значення:

Н.

Визначаємо силу тиску, що діє на поршень двигуна при самозайманні палива (приймаючи ):

(8.11)

Н.

Ззнаходимо максимальну силу, що діє на поршень у верхній мертвій точці (формула (8.9)):

Н.

Максимальний середній тиск на корінний підшипник колінчастого вала (сила Р розподіляється на два корінні підшипники):

(8.12)

МПа.

Визначаємо число Зоммерфельда, яке характеризує вантажопідйомність (несучу здатність) підшипника, за формулою:

(8.13)

Практично значення не перевершує 30.

Рідинне тертя в підшипнику забезпечується, якщо мінімальний зазор між підшипником і валом буде задовільняти умові:

(8.14)

де – критична товщина мастильного шару в підшипнику, м. Для автотракторних двигунів, що пройшли обкатку, можна приймати м;

– робоча мінімальна товщина шару мастила в підшипнику.

Мінімальний зазор між підшипником і валом для автомобільних двигунів можна приймати м, для тракторних дизелів м. Для СМД-14 приймаємо м.

Середній радіальний зазор у спряженні підшипник-вал визначається за формулою:

; (8.15)

мм= 6,6·10^-6 м.

Ексцентриситет вала в підшипнику:

; (8.16)

м.

Відносний ексцентриситет:

; (8.17)

_{Витрати мастила через зазори в підшипнику}

_{Тиск, що створюється у мастильному шарі, виштовхує мастило з торців підшипника.}

_{Витрати мастила з підшипника визначаємо згідно з ІСО 7902-1-2001:}

_{– створювані гідродинамічним тиском – за формулою:}

(8.18)

де – параметр витрат мастила з-за гідродинамічного тиску. Для (половинне охоплення цапфи вала мастилом) при , = 0,0679 (таблиця 9, сторінка 3 указаного стандарту). Приймаємо для розрахунку = 0,067. Отже:

м³/с;

_{–створювані тиском джерела мастила (М2) – згідно з рівняннями:}

(8.19)

де = 5/80=0,0625 – відношення діаметра отвору джерела мастила до ширини підшипника.

Отже:

(8.20)

де – параметр витрат мастила із-за тиску джерела мастила ( = 5·10⁵ Па);

(8.21)

м³/с;

–загальні витрати мастила:

М = М₁+М₂ = (17,07 +24,95)·10^-6 м³/с.

_{Витрати тепла в підшипнику}

_{Приймаємо тиск і температуру мастила на вході в підшипник і температуру на виході з нього.}

_{У таблиці 8.5 наведено значення тиску мастила джерела і температур мастила в підшипнику колінчастого вала для автотракторних двигунів.}

_{Таблиця 8.5 – Значення тиску джерела мастила і температур в підшипниках}

_{колінчастого вала автотракторних двигунів}

Двигуни	, МПа	Твх, 0С	Твих, 0С
Бензинові	0,3…0,4	70…75	90…95
Дизелі	0,4…0,6	75…80	80…110

_{Для дизеля СМД-14 приймаємо рп= 0,5 МПа; Твх = 75} ⁰_С;

_{Твих= 105} ⁰_{С. Середня температура в підшипнику Тс = (Твх + Твих) / 2 = 90} ⁰_С.

_{Визначаємо коефіцієнт тертя в підшипнику за формулою:}

(8.22)

де – коефіцієнт, який залежить від і відношення . Значення визначаються з графіка, який наведено на рисунку 8.3 [3].

Рисунок 8.3 – Номограма для визначення коефіцієнта

Для двигуна СМД-14 = 1,2. Отже, значення коефіцієнта тертя:

_{Кількість тепла, що виділяється в результаті тертя в підшипнику, визначаються за формулою:}

(8.23)

_{Н·м/с (Вт).}

_{Знаходимо температуру мастила на виході з підшипника, прийнявши її значення на вході Твх= 75} ⁰_{С і підвищення – на виході з підшипника}

_{на 30} ⁰_{С. Отже, Твих= 105} ⁰_С.

_{Середня температура мастила в підшипнику Тс = (Твх + Твих) / 2 = 90} ⁰_С.

_{При дисипації тепла від тертя через мастило, отримаємо температуру на виході за формулою:}

(8.24)

_{де µсV = 1,8·10}⁶ _Дж/(м³_{·К) – об’ємна питома теплоємність мастила.}

⁰С.

_{Визначаємо середнє значення температури в підшипнику для наступного наближення в розрахунках: Тс1 = (Твх + Твих1) / 2 = (75+ 93,9) / 2= 84,5} ⁰_С.

_{Далі знаходимо наступне наближення температури мастила на виході з підшипника:}

⁰С.

_{Наступна ітерація показала, що Твих2=108,09} ⁰_{С. Взагалі ітерації продовжуються до тих пір, поки різниця між наступним і попереднім значенням температури мастила на виході з підшипника буде меншою 2} ⁰_С.

_{У нашому випадку встановлено, що Твих= 108} ⁰_С.

_{Кількість тепла, що розсіюється у навколишнє середовище:}

(8.25)

де – тепло, яке випромінюється в навколишнє середовище;

Вт/(м³·К) – коефіцієнт, який характеризує тепловіддачу поверхнею корпусу підшипника;

– відповідно температури підшипника і оточуючого середовища;

– площа поверхні корпуса підшипника, ·D·l_n. Приймаємо для розрахунку = 20·88·10^-3·80·10^-3 = 0,1408 м². Попередньо у розрахунках приймаємо = 40 К.

_{Якщо прийняти, що все тепло тертя відводиться через поверхню корпуса підшипника (розсіювання тепла здійснюється лише шляхом конвекцїї), то:}

_{У цьому випадку, якщо прийняти Qf = Qc , температура поверхні корпусу підшипника:}

_{Tn = 1428,3 / 20·0,1408 + 40 = 547,2} ⁰_C.

_{Тобто дисипація тепла шляхом конвекції за відсутності тепловідводу з мастилом не забезпечить нормальні умови роботи підшипника.}

_{Кількість тепла, яке може бути відведено в результаті витоків з підшипника мастила, становить:}

(8.26)

Н·м /с (Вт).

Отриманий результат на 689,5 Вт є більшим від кількості тепла, що виділяється при терті в підшипнику, що свідчить про надійність тепловідводу мастилом і роботи підшипника.

Розглянутий метод розрахунку радіального підшипника ковзання за величинами К_ср і К_max наближений, оскільки він базується на критеріях подібності конструктивних параметрів (відносна довжина підшипника, діаметральний зазор) і експлуатаційних факторів (температура, в’язкість і тиск мастила) у двигуна, що проектується, і існуючого, подібного йому. Тому, використовуючи наведений метод, необхідно також проведення розрахунку підшипника на основі гідродинамічної теорії мащення.

Гідродинаміка радіального підшипника ковзання при фіксованому положенні лінії центрів підшипника і вала

Згідно з класичною гідродинамічною теорією мащення вал може займати різні положення в підшипнику. Проте у практиці реальних спряжень він має переважно фіксоване положення, наприклад, у ланцюгових, пасових передачах, колінчастих і розподільних валах двигунів внутрішнього згоряння тощо.

При значних зовнішніх навантаженнях на вал він також не має можливості займати різні положення в підшипнику. Те ж саме спостерігаємо у підшипниках з полімерних матеріалів у зв’язку з значними деформаціями подушки підшипника. Практично вал притискується до підшипника в одному місці і не може, у процесі роботи, зміщуватись, як це має місце у динамомашинах, турбогенераторах або інших подібних до них за умовами роботи машинах.

При розрахунках вантажності підшипників ковзання розподіл тиску в мастильному шарі підшипника, як правило, відшукують шляхом розв’язання відомих рівнянь Рейнольдса або Нав’є-Стокса у формі . У наведеній функції – розв’язок рівнянь для підшипника нескінченної довжини, – корегуюча функція, яка враховує скінченність довжини підшипника, – кутова координата, яка відраховується від лінії центрів і максимального зазору між підшипником і валом (розв’язок рівняння Рейнольдса Зоммерфельдом) або мінімального зазору в підшипнику (розв’язок рівнянь Нав’є-Стокса Лойцянським), Z– координата в осьовому напрямку (відраховується від середини підшипника).

Функція розподілу тиску по колу підшипника нескінченної довжини при відрахуванні від максимального зазору має наступний вигляд:

+

+ (8.27)

Якщо відлік кута здійснювати від мінімального зазору в підшипнику , то функція розподілу тиску буде мати наступний вигляд:

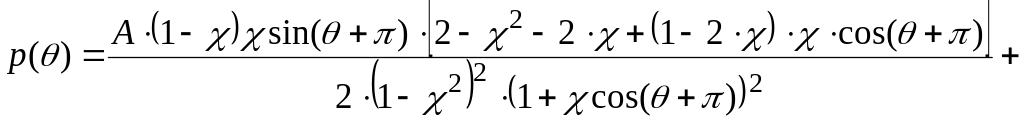+ (8.28)

Алгоритми визначення розподілу тиску мастила в підшипнику нескінченної довжини у системі MathCad і графіки розподілу тиску наведено на рисунку 8.5 (праворуч – функція Зоммерфельда).

Розрахункові параметри наступні: м/с, Н∙с/м², , м, м. При цьому Н/м² (вихідні дані, чисельні значення на графіках тут і далі наведено в системі СІ).

При фіксованому положенні лінії центрів вала в підшипнику:

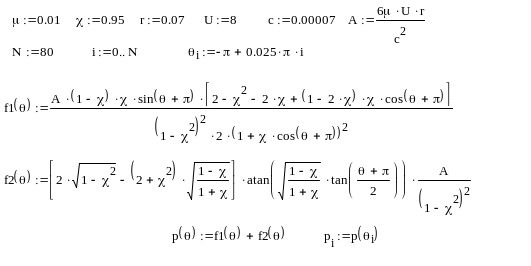
При використанні функції розподілу тиску, отриманої Зоммерфельдом:

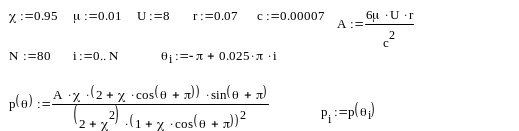
Рисунок 8.5 – Розподіл тиску по колу в підшипнику нескінченної довжини

У зоні джерела мастила (кишеня або отвір у подушці підшипника) при фіксованій величині зазору між підшипником і валом гідростатичний тиск має бути сталою величиною, що забезпечується для певного стану і режиму роботи двигуна сталою роботою мастильного насосу.

Для чисельних розрахунків приймемо наступне. В зоні джерела вздовж осі підшипника прорізано канавку шириною м, що відповідає центральному куту приблизно , тиск мастила в якій має стале значення Па (тиск мастила джерела) і зменшується за лінійним законом до нуля при , радіус шипа вала м (параметри близькі до відповідних параметрів для радіальних підшипників ковзання автотракторних двигунів).

Скористаємось функцією Хевісайда Φ(θ), за допомогою якої будемо корегувати розподіл гідростатичного і гідродинамічного тиску мастила по колу підшипника. У зоні джерела функція повинна фіксувати сталим гідростатичний тиск мастила, виключаючи одночасно там же гідродинамічний тиск. Указане можливо, якщо при і ; при .

Функція Хевісайда у цьому випадку має вигляд

Характер розподілу гідростатичного тиску по колу підшипника, корегований функцією Хевісайда, алгоритм визначення і графік розподілу тиску мастила по колу підшипника наведено на рисунку 8.6.

Рисунок 8.6 – Розподіл гідростатичного тиску по колу підшипника

Тиск мастила, отриманий в результаті додавання функцій гідродинамічного тиску, який виникає при обертанні вала в підшипнику на в’язкому мастилі і за наявності клинового зазору між цапфою вала і підшипником, і гідростатичного тиску в підшипнику, що створюється тиском мастила джерела, будемо називати гідростатодинамічним.

Функцію розподілу гідростатодинамічного тиску мастила по колу підшипника з урахуванням тиску мастила джерела отримаємо при додаванні функції, скорегованої функцією Хевісайда, (далі – ) і функції гідростатичного тиску .

На рисунку 8.7 наведено алгоритм визначення гідростатодинамічного тиску і графік його розподілу його по колу для підшипника нескінченної довжини.

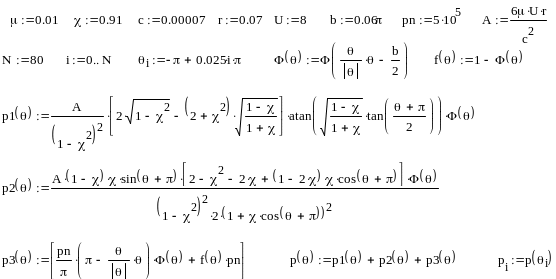
Рисунок 8.7 – Розподіл гідростатодинамічного тиску мастила в підшипнику нескінченної довжини

Змінюючи тиск мастила джерела і його конфігурацію, можна суттєво впливати на розподіл тиску мастила в підшипнику.

Наприклад, при тиску мастила джерела Па, відносному ексцентриситеті і, прийнятих, як для попереднього рисунку, розрахункових параметрах, отримуємо лише додатні значення тиску мастила по колу підшипника, тобто – повне охоплення цапфи вала мастилом.

Графік розподілу тиску мастила по колу в підшипнику в останньому випадку наведено на рисунку 8.8.

Рисунок 8.8 – Розподіл тиску мастила по колу підшипника з джерелом мастила

Можна отримати повне охоплення мастилом цапфи вала і при порівняно невисоких значеннях тиску мастила джерела.

Так, якщо в останньому випадку ширину щілини джерела збільшити у декілька разів (створити у підшипнику кишеню шириною ), то при p_n= 7·10⁵ Па отримаємо підшипник, наближений до гідростатичного, але з впливом на розподіл тиску і гідродинамічної компоненти (рисунок 8.9).

Рисунок 8.9 – Розподіл тиску мастила по колу підшипника з джерелом мастила за наявності кишені ( )