Модели, учитывающие сезонность
Сезонность можно учитывать, создавая модель временного ряда.
Эти ряды и их колебания можно представить как генерируемые моделями двух основных типов: моделями с мультипликативными и с аддитивными коэффициентами сезонности.
Модели первого типа имеют вид:
,
где
динамика величины
характеризует
тенденцию развития процесса;
,
,...,
—
коэффициенты сезонности;
—
количество
фаз в полном сезонном цикле (если ряд
представляет месячные наблюдения, то
в экономике обычно
=
12, при квартальных данных
=
4 и т. п.);
—
неавтокоррелированный
шум с нулевым математическим ожиданием.
Модели второго типа записываются как:
,
где величина описывает тенденцию развития процесса;
,
,...,
—
аддитивные коэффициенты сезонности;
— количество фаз в полном сезонном цикле;
— неавтокоррелированный шум с нулевым математическим ожиданием.
Адаптивная модель с мультипликативной сезонностью была предложена П. Р. Уинтерсом.
Аддитивная модель рассмотрена Г. Тейлом и С. Вейджем. Уинтерс поставил задачу разработать модель для прогнозирования объемов сезонных продаж с использованием ЭВМ. Модель должна быть такой, чтобы: а) прогнозы рассчитывались на основе одних и тех же программ для большого количества продуктов; б) вычисления производились быстро и дешево; в) использовался минимальный объем памяти для информации; г) учитывались изменяющиеся условия. Поэтому целесообразно в прогностических моделях учитывать конкретный характер тенденции и сезонных колебаний. Это и сделал Уинтерс с помощью экспоненциальной схемы. Модель при этом становится сложнее, зато и точность прогнозов для большинства товаров существенно возрастает.
Прогнозирование с коэффициентами сезонности
Данная модель содержит только сезонный эффект.
Модель имеет вид:
,
,
является
взвешенной суммой текущей оценки
,
полученной путем очищения от сезонных
колебаний фактических данных
и
предыдущей оценки
.
В качестве коэффициента сезонности
берется
его наиболее поздняя оценка, сделанная
для аналогичной фазы цикла. Затем
величина
,
полученная по первому уравнению,
используется для определения новой
оценки коэффициента сезонности по
второму уравнению.
Величины и могут быть записаны через прошлые данные и начальные условия:
,
где
—
начальное значение
;
—
начальное
значение
в
соответствующей
фазе
(месяце) цикла (года);
—
наибольшая
целая часть
.
8.Стохастические модели. Модель ariva. Стохастические модели с дискретным временем
Базовая модель динамики цен финансовых инструментов — модель геометрического броуновского движения , согласно которой доходности (непрерывные, логарифмические) инструментов подчиняются процессу случайного блуждания :
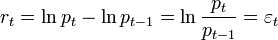
где 
— белый
шум
Данная модель удовлетворяет гипотезе эффективного рынка. В рамках данной гипотезы предполагается невозможность прогнозирования доходностей на будущие периоды на основании какой-либо информации, в том числе на основании информации о прошлых значениях доходностей.
В моделях ARIVA предполагается возможность прогнозирования доходностей на основе прошлых значений доходностей.
ARIVA – процессы Бокса-Дженкинса представляют собой довольно простые и гибкие линейные модели, которые могут неплохо описывать широкий спектр поведения различных временных рядов, в том числе и кратокосрочные, и среднесрочные всплески и падения, так называемого экономического цикла.
ARIMA
Авторегрессионное интегрированное скользящее среднее (autoregressive integrated moving average, ARIMA) является обобщением модели авторегрессионного скользящего среднего. Эти модели используются при работе с временными рядами для более глубокого понимания данных или предсказания будущих точек ряда. Обычно модель упоминается, как ARIMA(p,d,q), где p,d и q — целые неотрицательные числа, характеризующие порядок для частей модели (соответственно авторегрессионной, интегрированной и скользящего среднего).
Пусть
задан временной ряд 
,
где t —
целый индекс и
—
вещественные числа. Тогда модель
ARMA(p,q)
задаётся следующем образом:
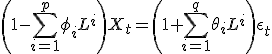
где L —
оператор задержки, 
—
параметры авторегрессионной части
модели, 
—
параметры скользящего среднего, а
—
значения ошибки. Обычно предполагают,
что ошибки
являются
независимыми одинаково распределёнными
случайными величинами из нормального
распределения с нулевым средним.
ARIMA(p,d,q) получается интегрированием ARMA(p,q).
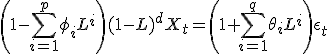
де d — положительное целое, задающее уровень дифференцирования (если d=0, эта модель эквивалентна авторегрессионному скользящему среднему). И наоборот, применяя почленное дифференцирование d раз к модели ARMA(p,q), получим модель ARIMA(p,d,q). Заметим, что дифференцировать надо только авторегрессионную часть.
Важно отметить, что не все сочетания параметров дают «хорошую» модель. В частности, чтобы получить стационарную модель требуется выполнение некоторых условий.
Существует несколько известных частных случаев модели ARIMA. Например, ARIMA(0,1,0), задающая
,
является моделью случайных блужданий.
Используется большое количество вариаций модели ARIMA. Например, если исследуются несколько рядов, то можно трактовать как векторы. Тогда мы приходим к модели VARIMA. Иногда в модели может иметься сезонный фактор. Примером может послужить модель объёма трафика за день. На выходных поведение ряда будет заметно отличаться от рабочих дней. В этом случае вместо того, чтобы наращивать порядки скользящего среднего и авторегрессионной части модели, лучше прибегнуть к модели сезонного авторегрессионного скользящего среднего (SARIMA). Если имеется некоторая долгосрочная зависимость, параметр d может быть заменён нецелыми значениями, приводя к авторегрессионному дробноинтегрированному процессу скользящего среднего (FARIMA или ARFIMA).