§2. Постановка задачі інтерполювання

Нехай – простір функцій з рівномірною нормою на множині . Нехай задано різні точки , і значення функції . Іншими словами, задано нерівномірну сітку і сіткову функцію . Нехай послідовність функцій простору – система лінійно незалежних функцій, а – підпростір розмірності узагальнених многочленів вигляду порядку з дійсними коефіцієнтами .

Задача інтерполювання ставиться таким чином: за заданим , знайти наближене значення функції як значення в точці узагальненого многочлена такого, що . Многочлен , який задовольняє останню умову, називається інтерполяційним многочленом для функції або інтерполюючою функцією. Точки називають вузлами інтерполювання. Наближену заміну функції многочленом називають інтерполюванням або інтерполяцією, а формулу , за допомогою якої обчислюють значення функції – інтерполяційною формулою.

Таким чином, щоб розв’язати задачу інтерполювання потрібно:

1. побудувати інтерполяційний многочлен;

2. обчислити його значення в точці .

У даній постановці задачі маємо справу з лінійним інтерполюванням, бо у параметри , які і визначають конкретний многочлен, входять лінійно. Якщо ж нелінійно залежить від параметрів, то інтерполювання називається нелінійним.

З геометричного змісту задача інтерполювання полягає у знаходженні кривої певного класу, яка проходить через точки площини з координатами .

Якщо функція належить класу алгебраїчних многочленів, то інтерполювання називається параболічним. Параболічне інтерполювання найзручніше, оскільки многочлени, які прості за формою і не мають особливих точок, можуть набувати довільних значень, їх легко обчислювати, диференціювати й інтегрувати.

У деяких випадках доцільніше використовувати інші класи інтерполюючи функцій. Якщо, наприклад, функція періодична, то функцію природно вибрати з класу тригонометричних многочленів, а якщо функція перетворюється на нескінченність у заданих точках або поблизу них, то функцію доцільно вибрати з класу раціональних функцій.

§3. Середньоквадратичне наближення функцій Нехай функцію задано таблично

х			...		...
			...		...

(1)

Потрібно побудувати многочлен , який у певному розумінні добре наближає таблично задану (дискретну) функцію (1) у випадку, коли . Найточніші значення коефіцієнтів визначають методом найменших квадратів. Цей метод запропонували відомі математики К.Гаусс та А.Лежандр.

Зокрема, К.Гаусс запропонував будувати такий многочлен для якого значення було б мінімальним. Можна було б вимагати щоб значення було мінімальним, але тоді наближення функції многочленом буде гіршим ніж у першому випадку.

Г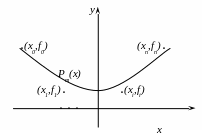 рафічна інтерпретація многочлену така: графік многочлена не пройде точно через точки , які належать графіку функції (на відміну від інтерполяції).

Графік проводиться так, щоб сума квадратів відхилень була найменшою (мінімальною): , де

Часто фізичний зміст задачі дає уявлення про форму кривої, яка відповідає конкретному фізичному закону, тоді з фізичних міркувань, для прикладу, випливає, що фізичний закон має лінійний характер, а результатів вимірювання вдосталь, то найрозумніше рівняння цього фізичного закону записати, користуючись многочленом середньоквадратичного наближення.

Для побудови многочлена, який здійснює середньоквадратичне наближення введемо таке позначення:

. (2)

Використовуючи явне представлення многочлена ми тепер можемо уточнити задачу про знаходження многочлена, який здійснює середньоквадратичне наближення: потрібно знайти такі коефіцієнти , щоб сума (2) була мінімальною. Ми, таким чином, одержали задачу про мінімізацію функції змінної, які ми позначили як .

Як відомо, мінімум виразу (2) одержимо, коли

(3)

Розписавши (3) та провівши відповідні скорочення, одержимо систему вигляду:

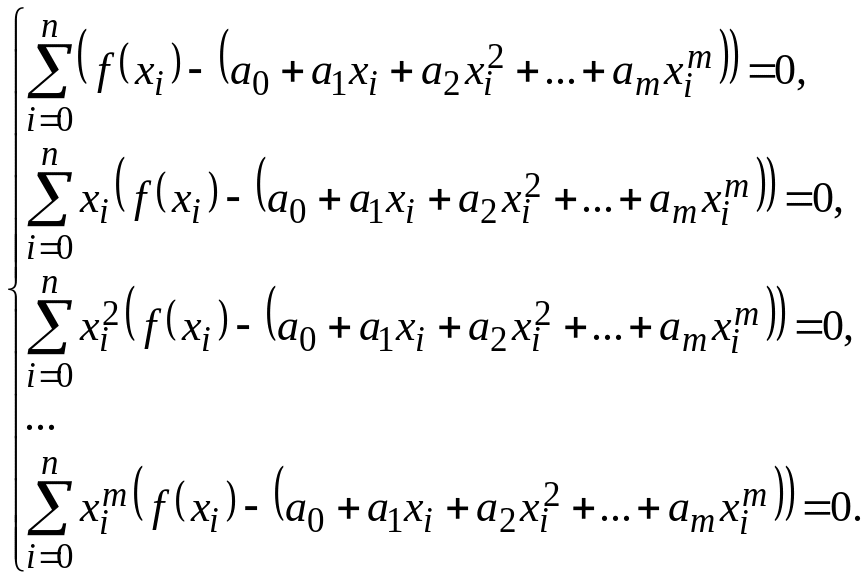(4)

В системі (4) кількість рівнянь і кількість невідомих рівна . Перепишемо цю систему у такому вигляді:

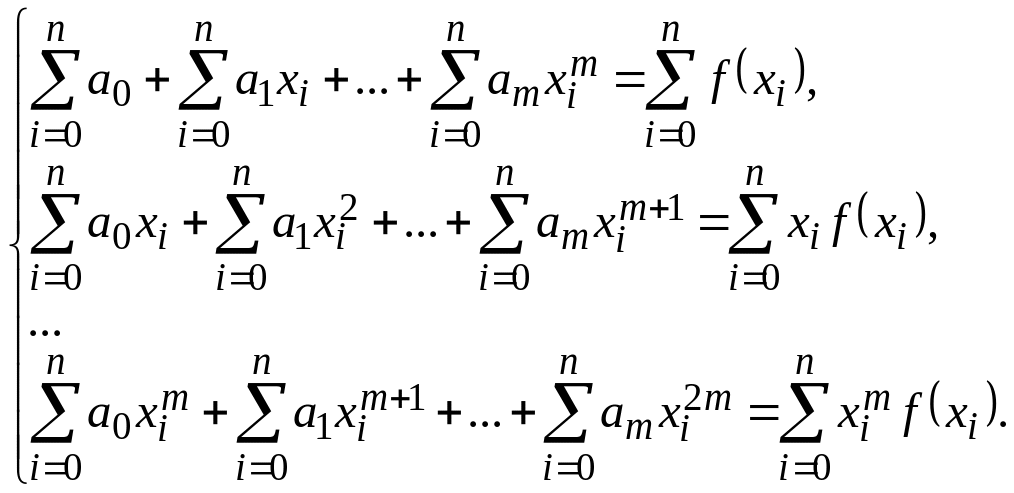(5)

В загальному випадку систему (5) запишемо так :

(6)

де

– невідомі коефіцієнти, .

Система вигляду (6) при великих важко піддається розв’язуванню. Інколи, матриця системи (6) є нестійкою. На практиці, при розв’язуванні системи (6) можна враховувати, що матриця симетрична, а тому слід використовувати метод квадратного кореня, який дасть менші похибки наближень.

Лінійне середньоквадратичне наближення одержимо у тому випадку, коли . Тобто, лінійне рівняння (пряма).

Тоді система рівнянь (6) матиме вигляд

яку розв’язавши методом Крамера знайдемо невідомі коефіцієнти, які підставивши у отримаємо многочлен найкращого лінійного середньоквадратичного наближення.