§3. Ітераційні методи для слар
Ітераційні
методи характеризуються тим, що розв’язок
СЛАР знаходиться у вигляді границі
деякої послідовності векторів, які
будуються за однаковим ітераційним
процесом. Перевагою ітераційних процесів
є те, що при побудові наступного наближення
враховується попереднє. Недоліком є
те, що ітераційний процес має обмежену
область застосування, може виявитися
розбіжним для даної системи або збіжність
буде дуже повільною, не дозволить досягти
потрібної точності. Ефективність
ітераційних методів визначається
швидкістю збіжності послідовних
наближень
до розв’язку
.
Член цієї послідовності
називається k-ою
ітерацією,
а k
– номером
ітерації.
Ітераційний
процес у канонічній формі для системи
(1) описується за допомогою схеми :
(2)
де
додаються матриці
і початкове наближення
.
Ітераційний
процес у формі (2) визначається системою
(1) і вибором матриць
і є загальним для ряду ітераційних
процесів. Якщо при обчисленні
використовується лише попередня ітерація
,
то ітераційний метод називається
однокроковим
або
двоярусним.
Ітераційні
процеси поділяються на стаціонарні і
нестаціонарні. Стаціонарні
– це такі процеси, в яких
не залежить від номеру ітерації k,
тобто
.
У нестаціонарних
процесах
для кожного номеру ітерації k
дістанемо свою матрицю
.
Ітераційний
метод називається збіжним,
якщо для деякої норми має місце рівність
.
Щоб
зупинити обчислення, задають деяке
число
,
яке є характеристикою похибки і обчислення
припиняють, коли
.
Вираз
називається нев’язкою, і завжди може
бути обчисленим. Нев’язка дає нам
порядок точності знаходження коренів
СЛАР.
Для зручності формувань лінійний однокроковий ітераційний метод записують у канонічній формі:
(3)
де
– деякі числові параметри. Якщо матриця
,
то метод (3) називається явним.
§4. Метод простої ітерації розв’язування слар Цей метод має вигляд
(4)
де
вибирається довільно. Метод простої
ітерації є явною однокроковою стаціонарною
схему із сталим параметром
.
У координатній формі (4) має вигляд
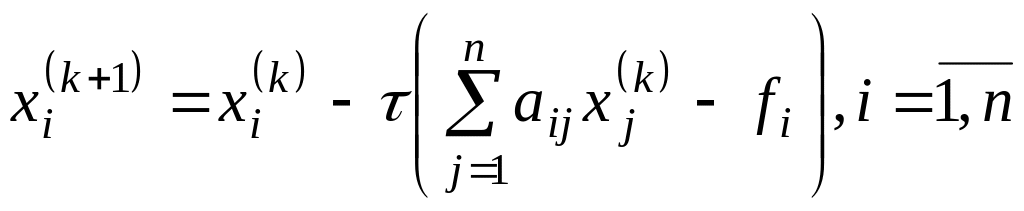
де
параметр
.
Метод
простої ітерації збігається коли
.
Метод простої ітерації зручно застосовується до тих СЛАР, в яких діагональні коефіцієнти перевищують інші коефіцієнти невідомих.
Тема ііi. Наближення функцій
§1. Наближення функцій
У процесі вивчення різних питань природознавства, економіки і техніки, соціології, педагогіки доводиться на основі великої кількості дослідних даних виявляти суттєві фактори, які впливають на досліджуваний об’єкт, а також встановлювати форму зв’язку між різними зв’язаними одна з одною величинами (ознаками).
Нехай
величина
є функцією аргументу
,
тобто будь-якому значенню
з області визначення цієї функції
поставлено у відповідність одне значення
.
Проте на практиці часто неможливо
записати цю функціональну залежність
у вигляді формули
.
У деяких випадках аналітичний вираз
хоч і відомий, але настільки громіздкий,
що його важко використовувати у практичних
розрахунках.
Нехай у результаті досліджень дістали таку таблицю деякої функціональної залежності:
х |
|
|
... |
|
у |
|
|
... |
|
Ці значення є або результатами обчислень, або експериментальними даними. Часто бувають потрібні значення функції і в інших точках, що не співпадають із точками . Проте у багатьох випадках одержати ці значення можна лише шляхом складних обчислень або проведенням дорогих експериментів.
Таким чином, з точки зору економії часу і коштів, ми приходимо до необхідності використання наявних табличних даних для наближеного обчислення значень функції . Тобто, потрібно знайти аналітичний вигляд функції , яка добре відображала б цю таблицю дослідних даних.