26. Понятие о дилатации.

Под дилатацией понимают предел отношения измененного элементарного объема, вызванного деформацией, к его первоначальной величине.

Рассмотрим

После деформации:

Т.о. первоначальный объем: , после деформации:

Относительное изменение объема:

Дивергенция вектора смещений будет отрицательной, если нормальные силы ориентирова­ны внутрь объема, и положительными - в противном случае.

имеют физический смысл сдвигов, т. е. выражают изменения формы.

Для малых перемещений связь между смеще­нием частицы и координатой можно считать линейной.

Общий сдвиг в плоскости XOY:

27. Тензор напряжений.

П усть p_X, p_Y, p_Z напряжения на гранях тетраэдра, ограниченных плоскостями YOZ, XOZ, XOY. Каждое из этих напряжений, в свою очередь, можно разложить на три компоненты по соответствующим координатным осям. Получаемые при этом девять скалярных величин (компонент напряжений) полностью определяют напряжение в окрестности точки M и составляют тензор напряжений:

В матрице первая буква индекса определяет грань, перпендикулярную соответствующей оси, вторая - компоненту напряжения на этой грани.

28. Физический смысл компонент тензора напряжений.

Компоненты напряжений с одинаковыми бу­квами в индексе (p_XX, p_YY, p_ZZ) направлены по нормали к соответствующим граням и называются нормальными напряжениями. Остальные шесть компонент называют касательными напряжениями. Причем: p_XY= p_YX, p_XZ = p_ZX, p_YZ = p_ZY.

29. Закон Гука.

Для идеально упругих сред установлена линейная зависимость деформа­ций от напряжений. Такая связь выражается линейным законом Гука, согласно которому де­формации прямо пропорциональны напряжениям. Согласно закону Гука, в общем случае неодно­родной среды каждая из шести компонент напряжения (p_XX, p_YY, p_ZZ, p_XY, p_XZ, p_YZ) является линей­ной функцией шести компонент деформации (e_XX, e_YY, e_ZZ, g_XY, g_XZ, g_YZ).

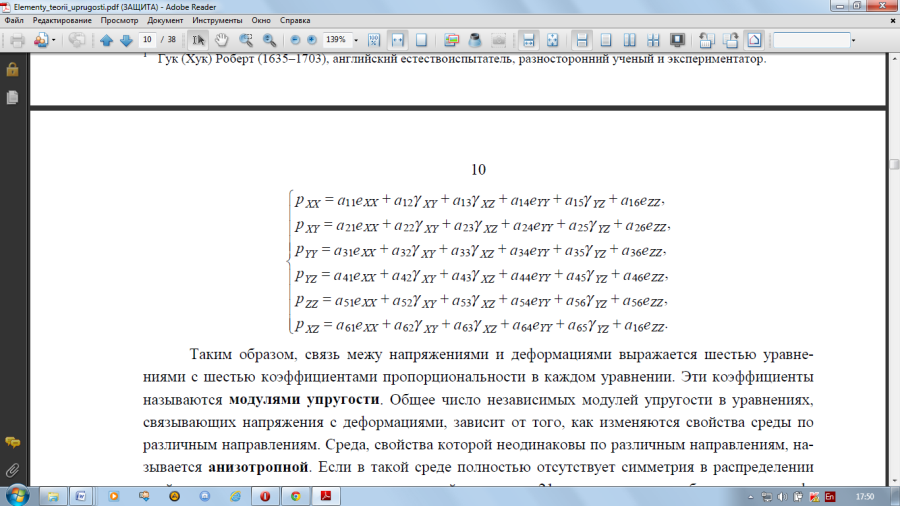
Таким образом, связь межу напряжениями и деформациями выражается шестью уравне­ниями с шестью коэффициентами пропорциональности в каждом уравнении. Эти коэффициенты называются модулями упругости a_ij.

Среда, свойства которой неодинаковы по различным направлениям, на­зывается анизотропной = 21. В случае изотропной сре­ды , где свойства одинаковы по всем направлениям, число упругих модулей = 2. Эти упругие модули λи μ называют коэффициентами упругости Ламе. Уравнения связи между напряжениями и деформациями в изотропной среде принимают вид:

Коэффициенты Ламе могут быть выражены через два других коэффициента упругости: мо­дуль Юнга (E) и коэффициент Пуассона υ.

Модуль Юнга E характеризует сопротивление горной породы растяжению или сжатию E=p_XX/e_XX.

Коэффициент Пуассона равен отношению относительного сжатия к относи­тельному расширению v=exx/e_YY.

Модуль сдвига μ характеризует сопротивление горной породы изменению формы при деформации μ=p_XY/exY, где p_XY - касательное на­пряжение, направленное вдоль оси Y; exY - угол сдвига грани параллелепипеда относительно оси X.

30. Системы упругих постоянных в теории малых деформаций абсолютно упругого тела.

31. Понятие о пластичности, упругом последствии и вязкости.

Упругое последействие - явление релаксации, состоящее в изменении с течением времени деформированного состояния твердого тела при неизменном напряженном состоянии. Упругое последействие характеризуется однозначностью условий равновесия (полная восстанавливаемость) между напряжением и деформацией, равновесное значение которой достигается по истечении достаточного времени. Различают прямое упругое последействие и обратное. Прирост дополнительной упругой деформации называют прямым упругим последействием, в отличие от обратного, где после устранения напряжения мгновенно снимается упругая деформация, а дополнительная упругая деформация асимптотически медленно исчезает во времени.

Пластичность структуры — это отношение соответствующих значений предельного напряжения сдвига к пластической вязкости

Пластическая вязкость - величина постоянная, не зависящая от напряжения сдвига и в осях координат градиент скоро­сти.

Вязкость — одна из важнейших технических характеристик нефти, продуктов её переработки, газовых конденсатов и фракций; определяет характер процессов извлечения нефти, её подъёма на дневную поверхность, промысловых сбора и подготовки, условия перевозки и перекачки продуктов, гидродинамического сопротивления при их транспортировании по трубопроводам и др. Для некоторых видов топлив и масел вязкость служит нормирующим показателем. 

32. Уравнение равновесия для идеально упругой среды.

Если рассматривать случай движения частиц среды, то в уравнение следует добавить силу инерции, которая согласно второму закону Ньютона для единичной массы равна , тогда уравнение движения среды следует записать в следующем виде:

33. Волновое уравнение в перемещениях.

Элементарный объем среды находится в состоянии равновесия (покоя), если сумма всех действующих на него сил (поверхностных и объемных) равен нулю. Для составляющих сил, дей­ствующих вдоль координатных осей X, Y, Z это условие определится уравнениями: £ F _X = 0; ZZ F_Y = 0; ZZ F_Z = 0. В развернутом виде эти уравнения следует записать в виде:

Если рассматривать конечный объем W и охватывающую его поверхность S, то каждое из уравнений системы следует записать в интегральной форме.

Преобразовав поверхностный интеграл в с помощью формулы Остроградского-Гаусса в объемный, уравнений следует записать в виде:

34. Волновое уравнение в напряжениях.

Волновое уравнение можно записать через компоненты смещений u, v, w. Учтем также, что в однородной изотропной среде λ = const, µ=const, ν=const.

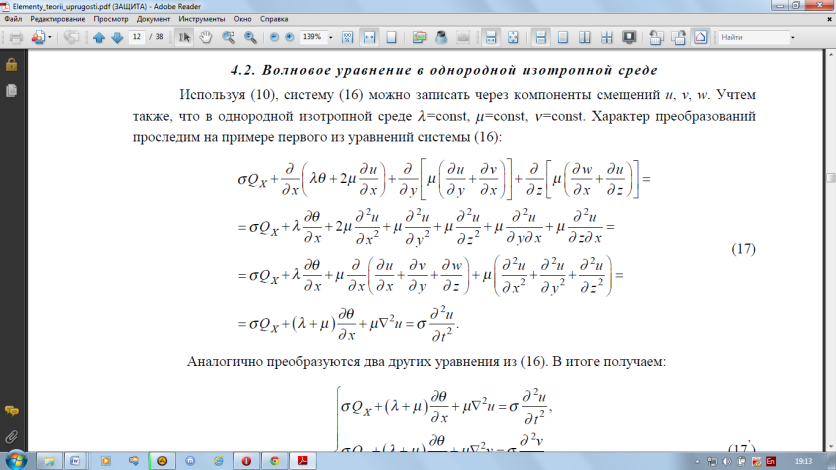
Продолжа преобразования, получим:

Три скалярных уравнения могут быть записаны в виде одного векторного :

При больших удалениях от внешнего источника, внешние силы = 0, в это случае:

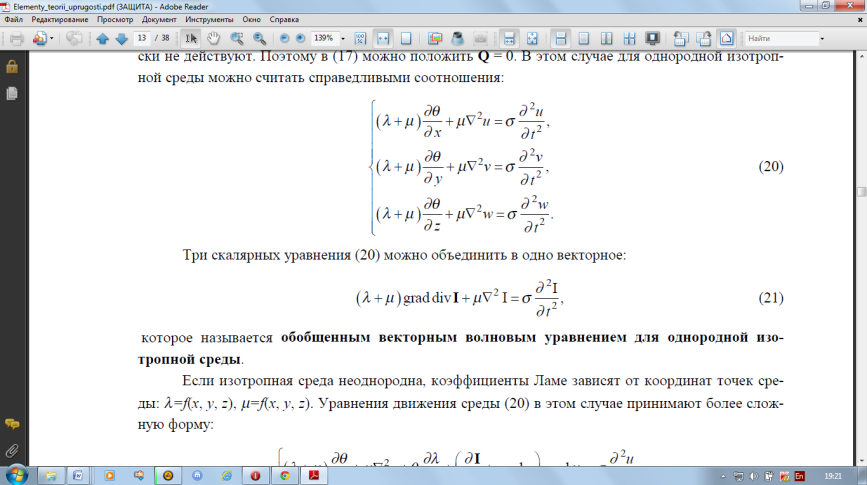- обобщенным векторным волновым уравнением для однородной изо­тропной среды

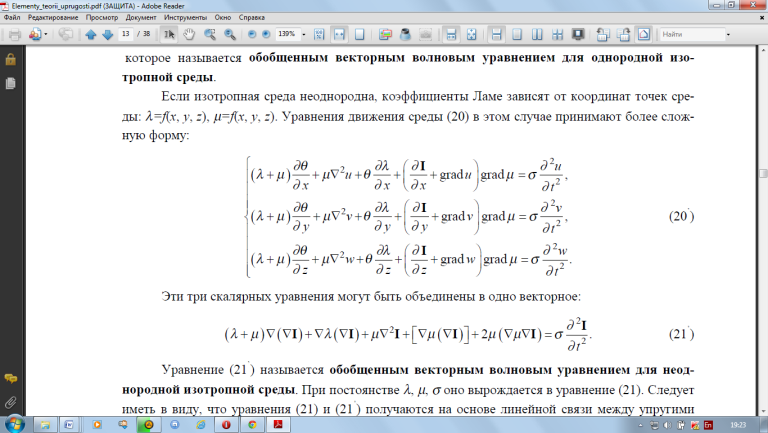
Если среда изотропна но не однородна уравнение примет вид:

35. Постановка задач о распространении волн.

36. Начальные и граничные условия в задачах о распространении волн.

Если требуется определить поле смещений в интервале времени [0, t_m], то начальные условия сводятся к заданию потенциала и его производной для момента времени t = 0.

Где ищется решение:

Если до момента t=0 смещения в среде отсутствовали, эти условия задаются в следующем виде:

- это начальные условия.

Граничные условия включают в себя краевые условия и условия сопряжения. Краевые условия задаются на поверхности S, ограничивающей область V, в которой ищется решение. Способ задания этих условий может быть различным. В зависимости от характера задачи на поверхности S могут быть заданы потенциал и его нормальная производная, смещения, либо напряжения. На одной части поверхности могут быть заданы напряжения, а на другой части - смещения. Условия сопряжения, то они определяют поведение поля на особых поверхно­стях, где происходит скачкообразное изменение упругих свойств среды.