Линейные операции над векторами

Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.

Пусть а и b — два произвольных вектора. Возьмем произвольную точку О и построим вектор ОА=а. От точки А отложим вектор АВ = b . Вектор ОВ, соединяющий начало первого вектора с концом второго, называется суммой векторов а и b : О B=а+b (см. рис. 2)

.

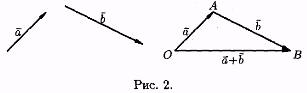Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелoграмма (см. рис. 3).

На рисунке 4 показано сложение трех векторов а, b и с.

 

Под разностью векторов а и b понимается вектор с=а-b такой, что b+с=а (см. рис. 5).

 

Отметим, что в параллелограмме, построенном на векторах а и b одна направленная диагональ является суммой векторов а и b , а другая — разностью (см. рис. 6).

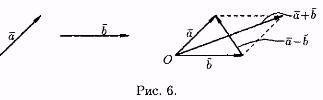
Можно вычитать векторы по правилу: а - b = а + (-b ), т. е. вычитание векторов заменить сложением вектора а с вектором, противоположным вектору b .

Произведением вектора а на скаляр (число) λ  называется вектор λ*а (или а*λ), который имеет длину    |λ|*|а|, коллинеарен вектору а, имеет направление вектора а, если λ>0 и противоположное направление, если λ<0. Из определения произведения вектора на число следуют свойства этого произведения:

1) если b=λ * а , то b || а . Наоборот, если b ||а , (а0 ), то при некотором λ  верно равенство b = λа ;

2)    всегда а =|а | • а ^-о , т. е. каждый вектор равен произведению его мо дуля на орт.

Линейные операции над векторами обладают следующими свойствами:

1.    а+b=b+а 2.    (а +b)+с=а +(b +с), 3.    λ1 • (λ2 •а) =λ1 •λ2 •а, 4.      (λ1 +λ2) •а =λ1 •а +λ2 •а, 5.    λ • (а +b) =λ •а+λ •b.

Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.

Проекция вектора на ось

Пусть в пространстве задана ось l, т. е. направленная прямая.

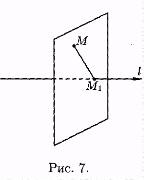
Проекцией точки М на ось l называется основание М₁ перпендикуляра ММ₁, опущенного из точки на ось.

Точка М₁ есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).

Если точка М лежит на оси l, то проекция точки М на ось совпадает с М1.

Пусть АВ — произвольный вектор (АВ 0). Обозначим через А₁ и b ₁проекции на ось l соответственно начала А и конца В вектора АВ и рассмотрим вектор А₁В₁

Проекцией вектора АВ на ось l называет ся положительное число |A ₁B ₁ | , если вектор А ₁В ₁ и ось l одинаково направлены и отрица тельное число — |A ₁B ₁ | , если вектор А ₁В₁ и ось l противоположно направлены (см. рис. 8). Если точки a ₁и b ₁совпадают (А ₁В ₁ =0), то проекция вектора АВ равна 0.

Проекция вектора АВ на ось l обозначается так: пр_lАВ. Если АВ=0 или АВl , то пр_l АВ=0.

Угол   между вектором а и осью l (или угол между двумя векторами) изображен на рисунке 9.

5. Скалярное произведение векторов

Определение. Скалярным произведением векторов   и   называется число, равное произведению длин этих сторон на косинус угла между ними.

  Свойства скалярного произведения:               

Скалярное произведение в координатах  Если     то   

Векторное произведение векторов.Определение. Векторным произведением векторов  и   называется вектор  , удовлетворяющий следующим условиям:

1)  , где ⱷ - угол между векторами  и  ,

2) вектор  ортогонален векторам  и 

3)  ,  и   образуют правую тройку векторов.

Обозначается:   или .

Свойства векторного произведения векторов:

1)  ;

2)  или  = 0 или  = 0;

3) (m ) =  (m ) = m( );

4)  ( +  ) =  +    ;

5) Если заданы векторы  (x_a, y_a, z_a) и  (x_b, y_b, z_b) в декартовой прямоугольной системе координат с единичными векторами  , то

* = 6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах  и  .

6. Дивергенция —это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.

Оператор дивергенции, применённый к полю  , обозначают как

или .

Определение дивергенции:

где Ф_F — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся кнулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной о перацией и для чего очевидно недостаточно стремления к нулю площади поверхности и объёма ее внутренности). В обоих случаях подразумевается, что

.

Физический  смысл дивергенции.

Выясним с помощью формулы  div F(M)=lim((V)→0) 1/(V) ∫s∫(V, n)ds  физический смысл дивергенции. Для этого будем рассматривать векторное поле F(M)  как поле скоростей жидкости с плотностью р==1. Как установ­лено поток П=∫s∫(V, n)ds

вектора F(M) равен количеству жидкости, протекающей за еди­ницу времени через поверхность S в направлении нормали n. Пусть n — внешняя нормаль. Поскольку S — замкнутая поверхность, то очевидно  поток вектора F(M)  равен количеству жидко­сти, которое за единицу времени возникает или уничтожается в пределах области V, ограниченной поверхностью S. Назовем это количество суммарной мощностью источников (если П>0) или стоков (если П<0), расположенных в области V. Рассмотрим отношение1/(V) ∫s∫(V, n)ds. Оно представляет собой среднюю плотность источников (или сто­ков) , т. е. количество жидкости, возникающей (или исчезающей) за единицу времени в единице объема области V, а предел lim((V)→0) 1/(V) ∫s∫(V, n)ds  при условии, что область V стягивается в точку М, можно назвать плотностью источников (или стоков) в точке М. Но этот предел равен div F(M). Таким образом, дивергенция векторного поля скоростей характеризует плотность источников жидкости.

Если div F(M )>0, то, как следует из формулы ∫v∫∫ div F(M)dv=∫s∫( F(M)n)ds , П>0, т. е. внутри области V имеются источники жидкости и из нее вы­текает жидкости больше, чем втекает; если div F(M )>0, то П<0, т. е. внутри области V имеются стоки жидкости и в нее вте­кает жидкости больше, чем вытекает. Если же div F(M )=0, то П=0, т. е. внутри области V нет ни стоков, ни источников и в нее втекает столько же жидкости, сколько и вытекает. Это, на­пример, имеет место для любой области V, расположенной в по­токе воды, текущей в реке. Для произвольного векторного поля div F(M) =0 имеет аналогич­ный физический смысл: дивергенция характеризует плотность источников поля.

Векторное поле F(M) наз соленоидальным или трубчатым , если в каждой его точке  дивер. div F(M )=0. Вычислим дивергенцию div(M ): V(M)= {-ω_y, ω_x, 0}; div V(M)= ∂V\∂x+∂V\∂y+∂V\∂z=∂( -ω_y)\∂x+∂(ω_x)\∂_y+∂0\∂z=0- векторное поле соленоидальное.