1. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

Формуле   (6.1)   можно   придать   иной   вид.   Так   как | a| cos=пр _ba, (см. рис.14), a |b| cos = пр _ab, то получаем:

      

 т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Использование скалярного произведения крайне широко, как в элементарных, так и в весьма абстрактных областях математики, физики и прикладных наук.

Широко известны следующие применения:

Любые геометрические вычисления, связанные с длинами, углами, проецированием, ортогональностью.

Например, 

• теорема косинусов легко выводится с использованием скалярного произведения:

• Угол между векторами:

• Оценка угла между векторами: в формуле   знак определяется только косинусом угла. Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

• Проекция вектора 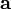  на направление, определяемое единичным вектором  : ,

• условие ортогональности^[2] (перпендикулярности) векторов   и  : итд.

• Площадь также выражается через скалярное произведение, например, двумерная площадь параллелограмма, натянутого на два вектора   и  , равна

Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.

Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. са и сb;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е. 

3.Векторы a, b и с образуют правую тройку.

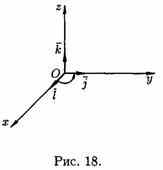
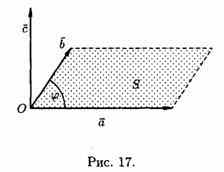
Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k,    j х k = i,    k х i = j.  Докажем, например, что iхj=k.

1) ki, kj;

2) |k|=1, но | i x j| = |i| • |J| • sin(90°)=1;

3) векторы i , j и k образуют правую тройку.

21. Малые напряжения и малые деформации.

В твердых и жидких средах под действием внешних сил распространяются слагающие тело частицы.

Частные случаи распространения волн.

Горные породы как физические объекты рассматриваются в виде непрерывной совокупности отдельных частичек и процессов описывающих законами классической механики. любые смещения элементов среды, которые вызывают изменение смещения формы называются деформациями. Если после прекращения сил деформации не восстанавливаются называются не упругими. Если произошло полное восстановление формы и размеров, то деформация – упругая.

Для малых деформаций характерных колебаний земной коры, деформации считаются упругими, а волны называются сейсмическими.

Упругие деформации.

Пусть переходит в Компоненты вектора смещения I по осям x;y;z являются функциями координат U(x;y;z); V(x;y;z); W(x;y;z).

Тогда значения компонент смещения в точке Q имеет вид:

Частные производные - это относительные удлинения/укорочения вдоль соответствующих осей x;y;z.

- это относительное удлинение по оси 0z.

Через относительное удлинение могут быть выражены изменения всего элементарного объема среды.

Внешние силы могут быть приложены к поверхности тела (поверхностные-внешние силы воздействия на поверхности изучаемой среды) или к каждому элементу объема (объемные-гравитационная сила, возникающая внутри каждой точки).

Для тела находящегося в равновесии действие внешних сил компенсируется внутренними силами. Такой процесс порождает в теле внутреннее напряженное состояние, представляющую реакцию тела на действие силы. Рассмотрим распределение сил

Ч тобы В осталась в том состоянии, то на S надо создать систему поверхностных сил, заменяющих действие на В части А. Они определяют то напряжение состояния, которые действовало в точках тела, до его рассечения.

Вектор силы зависит от вектора рассечений.

2. Ра́диус-ве́ктор — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат.

Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.

Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.

На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

Радиус-вектор в различных системах координат:

• Декартовы:

• Полярные, цилиндрические и сферические:

4. Вектор - это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А — начало вектора, а В - его конец, то вектор обозначается символом АВ или а. Вектор ВА (у него начало в точке В, а конец в точке A ) называется противоположным вектору АВ . Вектор, противоположный вектору а , обозначается -а .

Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени изменяется от точки к точке и может быть описан векторным полем