2. Дифференциал. Инвариантность формы записи дифференциала

Пусть функция y=f(x) определена и дифференцируема в т. , т.е. , это значит, что переменная отличается от предела y’ на б.м.в. (при ).

Т.е. или – приращение функции.

Если .

Произведение двух б.м.в. есть б.м.в. более высокого порядка малости, чем , т.е. .

Т.о. .

Более того, б.м.в. и эквиваленты, т.е. предел их отношения равен единице, т.е.

~ .

Note 1

В приближенных методах вычисления используется запись .

Т.	Если две б.м.в. эквиваленты, то каждая из них является главной частью другой. Т.е. если α ~ β ( при ), то

Proof:

Пусть α ~ β , тогда по лемме переменная отличается от предела 1 на б.м.в., т.е.

, где γ – б.м.в. (если ).

Откуда , но - б.м.в. более высокого порядка малости, чем , т.е. , ч.т.д.

Note 2

Дома или на п/з аналогично доказать, что .

Def.	(Наизусть!) Дифференциалом функции y=f(x) в т. называют главную, линейную относительно приращения аргумента часть приращения функции, т.е. если , то – дифференциал функции.

Note 3

В математике принято приращение аргумента считать дифференциалом аргумента, т.е. , тогда . Откуда – читается «дэ игрек по дэ икс».

Note 4

Следовательно, если , то ; если , то и т.д.

Note 5

Дома или на п/з составить таблицу дифференциалов элементарных функций .

Инвариантность формы записи дифференциала

1. Пусть x – основной аргумент функции y=f(x), .

Тогда дифференциал .

2. Пусть x – промежуточный аргумент сложной функции y=y[x(t)].

Тогда по определению дифференциала , или, учитывая формулу дифференцирования сложной функции , получим

,

т.е. формула записи для дифференциала не изменилась. Это свойство дифференциала называют инвариантностью:

.

3. Геометрический смысл производной и дифференциала

Пусть на плоскости с д.п.с.к. X0Y определена и дифференцируема функция y=f(x) в некоторой области т. .

1. Тогда приращение функции .

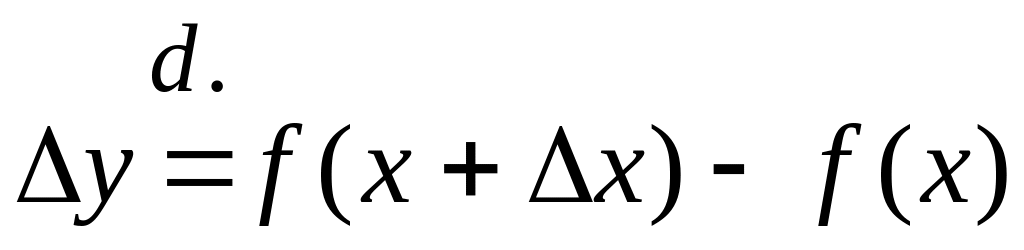2. Приращение касательной .

Действительно, пусть две точки M и N принадлежат кривой L.

Def.1

Секущей называют прямую, проходящую через любые две точки кривой.

Def.2

Касательной к кривой L в т. M называют предельное положение секущей при N→M.

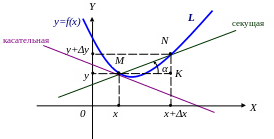
Пусть кривая L в д.п.с.к. X0Y задана явно y=f(x).

Тогда из прямоугольного , если т. N → т. M, то , или угловой коэффициент касательной

.

Пусть т. M₀ (x₀, y₀) L, тогда уравнение прямой, проходящей через т. М₀ с заданным угловым коэффициентом k , имеет вид

уравнение касательной.

Пусть нормаль – прямая, проходящая через т. М₀ перпендикулярно касательной, тогда

уравнение нормали.

Note !

Дифференциал геометрически равен приращению касательной, в отличие от приращения функции.

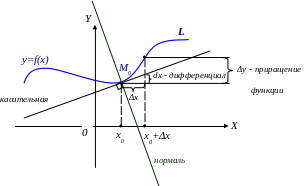
Note !

Следует заметить, что (в зависимости от выпуклости или вогнутости графика функции y=f(x)) дифференциал dy может быть как меньше, так и больше приращения функции. Однако в любом случае дифференциал – главная, линейная его часть.