22. Случайная величина и её числовые характеристики.

Одним из основных понятий в теории вероятностей является понятие случайной величины, под которой будем понимать некоторую величину, принимающую в зависимости от случая те или иные значения с определенными вероятностями.

Различают два вида случайных величин: дискретные и непрерывные.

Дискретной назовем случайную величину, принимающую изолированные друг от друга значения, которые можно пронумеровать.

Обычно дискретная случайная величина используется при описании измерений, принимающих целочисленные значения (например, количество отличных оценок у студентов одной группы на экзамене; число растений спелой ржи на 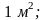количество деталей высокого качества, сошедших с конвейера в течение смены и т. д.).

Непрерывной будем называть случайную величину, возможные значения которой заполняют некоторый числовой промежуток (например, глубина заделки семян при посеве; погрешность при измерении той или иной величины; периметр перпендикулярного сечения ствола дерева и т. д.).

23. Законы распределения случайных величин.

Биномиальное распределение. К этому распределению приводит схема Бернулли. Пусть производится независимых повторных испытаний, в каждом из которых вероятность появления события постоянна и равна Тогда случайная величина 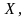 означающая число появления события в испытаниях, может принимать значения с вероятностями, вычисляемыми по формуле Бернулли:

, где

Такое распределение дискретной случайной величины 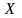называют биномиальным.

Параметрами биномиального распределения являются   и  Кратко биномиальное распределение с параметрами  и   записывают в виде 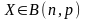. Математическое ожидание и дисперсия биномиальной случайной величины соответственно равны:

Распределение Пуассона. Если в биномиальном распределении вероятность события (или ) в одном испытании равна (или ) и очень мала, но число испытаний достаточно велико, причем произведение сохраняет постоянное значение (то есть среднее число появления события в различных сериях испытаний остается неизменным), а именно 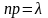, то случайная величина — число появлений события в опытах — может принимать значения с вероятностями, вычисляемыми по формуле Пуассона:

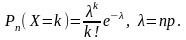
Такое распределение дискретной случайной величины называется распределением Пуассона. Параметром распределения Пуассона является постоянная величина , которой равны как математическое ожидание так и дисперсия, то есть Поэтому распределение Пуассона может служить оценкой точного биноминального распределения дискретной случайной величины, если ее математическое ожидание мало отличается от дисперсии, то есть

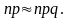
Равномерное распределение. Непрерывная случайная величина называется равномерно распределенной на отрезке , если плотность вероятностей этой величины постоянна на данном отрезке и равна нулю вне этого отрезка.