Тема 6. Обобщенный метод наименьших квадратов. Теорема Айткена. Фиктивные переменные. Построение регрессионных моделей по неоднородным данным. Тест Чоу.

При эконометрическом моделировании реальных экономических процессов предпосылки КЛММР нередко оказываются нарушенными: дисперсии остатков модели не одинаковы (гетероскедастичность остатков), или наблюдается корреляция между остатками в разные моменты времени (автокоррелированные остатки). Тогда предпосылка 3 запишется следующим образом:

3. М(εε^Т)=Ω, где Ω – положительно определенная матрица.

Принимая, что дисперсии объясняющих переменных могут быть произвольными, мы получаем обобщенную линейную модель множественной регрессии (ОЛММР).

В этом случае оценка параметров модели методом наименьших квадратов даст неэффективную оценку, поэтому следует применять обобщенный метод наименьших квадратов (ОМНК).

Теорема Айткена. В классе линейных несмещенных оценок вектора β для обобщенной регрессионной модели оценка b* =(X^ТΩ^-1X)^-1X^ТΩ^-1Y имеет наименьшую ковариационную матрицу.

Если модель гетероскедастична, то матрица Ω – диагональная. Тогда имеем:

b* =(X^ТΩX)^-1X^ТΩY.

В этом случае обобщенный метод наименьших квадратов называется взвешенным методом наименьших квадратов, поскольку мы «взвешиваем» каждое наблюдение с помощью коэффициента 1/σ_i.

На практике, однако, значения σ_i почти никогда не бывают известны. Поэтому сначала находят оценку вектора параметров обычным методом наименьших квадратов. Затем находят регрессию квадратов остатков на квадратичные функции объясняющих переменных, т.е. уравнение

е²_i =f(x_i) + u_i, i = 1, …, n,

где f(x_i) – квадратичная функция.

Далее по полученному уравнению рассчитывают теоретические значения и определяют набор весов 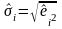. Затем вводят новые переменные Y^*_i = Y/σ_i, X^*_ji = X_ji/σ_i, (j = 1,…,m; i = 1,…, n) и находят уравнение 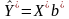. Полученная оценка и есть оценка взвешенного метода наименьших квадратов.

При изучении социально-экономических процессов и явлений может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровня, например, образование, пол, фактор сезонности. Качественные признаки могут существенно влиять на структуру линейных связей между переменными и приводить к скачкообразному изменению параметров регрессионной модели. В этом случае говорят об исследовании регрессионных моделей с переменной структурой или построении регрессионных моделей по неоднородным данным.

Оценить влияние значений количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии можно путем введения фиктивных переменных.

В качестве фиктивных переменных обычно используются дихотомические (бинарные) переменные, которые принимают всего два значения: «0» и «1». Например, при исследовании зависимости заработной платы от уровня образования Z можно рассмотреть k=3 уровня: начальное образование, среднее и высшее. Обычно вводят (k-1) бинарную переменную. В нашем случае потребуется ввести две фиктивные переменные.

Тогда регрессионная модель запишется в виде:

y= b₀ + b₁∙x₁ + … + b_m∙x_m + b_m+1∙z₁ + b_m+2∙z₂ +ε,

где

x₁, …,∙x_m – экономические (количественные) переменные.

Наличие у работника начального образования будет отражено парой значений z₁=0, z₂=0.

Параметры при фиктивных переменных z₁ и z₂ представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы (в нашем примере это работники с начальным образованием).

При построении регрессионных моделей по неоднородным данным необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле, можно ли объединить их в одну и рассматривать единую модель регрессии?

Для ответа на этот вопрос можно воспользоваться тестом Г.Чоу.

По каждой выборке строятся две линейные регрессионные модели:

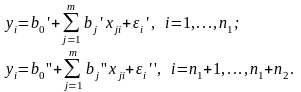
Проверяемая нулевая гипотеза имеет вид – H₀: b'=b''; D(ε')= D(ε'')= σ².

Если нулевая гипотеза верна, то две регрессионные модели можно объединить в одну объема n = n₁ + n₂.

Согласно критерию Г.Чоу нулевая гипотеза H₀ отвергается на уровне значимости α, если статистика

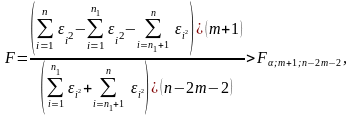
где 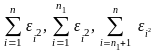- остаточные суммы квадратов соответственно для объединенной, первой и второй выборок, n = n₁ + n₂.

Для проверки гипотезы о структурной стабильности тенденции изучаемого временного ряда можно также использовать тест Д.Гуйарати.

Пример 4. Рассмотрим полученную в примере 1 модель зависимости балансовой прибыли предприятия торговли  (тыс. руб.) от следующих переменных:

- фонд оплаты труда, тыс. руб.; - объем продаж по безналичному расчету, тыс. руб.

Известно, что первая выборка значений переменных объемом n₁=12 получена при одних условиях, а другая, объемом n₂=12, - при несколько измененных условиях.

Задание: Проверьте, адекватно ли предположение об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки в одну и рассматривать единую модель регрессии по ?

Решение.

Для проверки предположения об однородности исходных данных в регрессионном смысле применим тест Чоу.

В соответствии со схемой теста построим уравнения регрессии по первым n₁=12 наблюдениям. Результаты представлены в таблице 8.

Таблица 8

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	1,02E+09	5,1E+08	11,9033	0,002967
Остаток	9	ESS1 = = 3,85E+08	4,3Е+07
Итого	11	1,40E+09

Результаты дисперсионного анализа модели, построенной по оставшимся n₂=12 наблюдениям, представлены в таблице 9.

Таблица 9

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	1,87Е+09	9,33E+08	57,1758	7,6549E-06
Остаток	9	ESS2 = = 1,47E+08	1,63Е+07
Итого	11	2,01E+09

Результаты регрессионного и дисперсионного анализа модели, построенной по всем n = n₁ + n₂ = 24 наблюдениям, представлены в таблице 3 (ESS = 6,39Е+08):

Рассчитаем статистику F по формуле:

^.

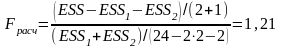Находим табличное значение F_табл= FРАСПОБР(0,05;3;18) = 3,15.

Так как, F_расч< F_табл, то справедлива гипотеза , т.е. надо использовать единую модель по всем наблюдениям. 