Тема 1. Понятие экономической модели. Роль моделей в экономической теории и принятии решений. Типы экономических моделей. Неполнота в экономических моделях. Основные этапы построения экономических моделей.

Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды, или какое следует предпринять действие для получения возможно лучшего финансового результата.

Необходимость использования математических методов в экономике в целом и таможенном деле в частности диктуется тем, что последствия принимаемых решений могут касаться большого числа людей и быть связаны с огромными затратами. Поэтому степень ответственности за принимаемые решения значительно возрастает. Перевод реального мира коммерческой деятельности на язык математики позволяет получить наиболее точное представление о его существенных свойствах и предсказать будущие события.

Специалисты в области экономических исследований считают, что дальнейший прогресс тесно связан с более широким использованием математических методов и моделей. Если раньше доминировал качественный анализ, то теперь выявлены количественные закономерности и построены математические модели многих экономических явлений и процессов. В результате наблюдается более глубокое проникновение в сущность изучаемых процессов, в саму природу явлений. Смелые замыслы познания математиков в макро- и микромире позволяют получать удивительные результаты. Например, некоторые закономерности были найдены чисто математическим путем, в то время как непосредственное наблюдение не позволило установить даже их присутствие. Поэтому путь математического моделирования экономических процессов и последовательного установления логических причинно-следственных связей для обеспечения возможности наблюдения, контроля и управления ими есть наиболее эффективное средство для решения различных проблем. Предложенные суждения о математике как об инструменте исследования в различных сферах человеческой деятельности являются результатом оценки потребителя с позиций ее полезности и ценности для развития общества в будущем.

Количественный аспект анализа экономических явлений и процессов всегда занимал большое место в работах классиков отечественной и зарубежной экономики. Например, еще в 1938 г. Французский математик Курно в работе «Исследование математических принципов теории богатства» сформулировал «закон спроса».

Коммерческая деятельность связана с постоянным поиском наиболее выгодного варианта распределения различного вида ресурсов: финансовых, трудовых, товарных, технических, энергетических, информационных и др. В настоящее время усложнение взаимосвязей вне и внутри коммерческих предприятий, наличие большого числа показателей, факторов и ограничений, а также быстрый рост конкуренции не позволяют оперативно сформировать оптимальный план без применения специальных методов. Кроме того, время решения задач обычно ограничено, и поэтому не всегда составляется лучший план действий.

Существующие математические модели и методы позволяют решать задачи большой размерности и учитывать широкий перечень показателей и факторов влияния, а время решения задач значительно сокращается с применением компьютерной технологии обработки информации.

Математические методы используются при прогнозировании таких важных показателей как валовой национальный продукт, уровень безработицы, темп инфляции и дефицит федерального бюджета, а также позволяют давать перспективные прогнозы о состоянии потребительского рынка, товарных рынков, регулируют динамику цен.

Существует три основных класса моделей, которые применяются для анализа или прогноза.

1. Модели временных рядов, включающие модели:

- тренда: y(t) = T(t) + _t, где T(t) – временной тренд заданного параметрического вида, _t - случайная компонента;

- сезонности y(t) = S(t) + _t, где S(t) – периодическая (сезонная) компонента, _t - случайная компонента;

- тренда и сезонности y(t) = T(t) + S(t) + _t, (аддитивная);

y(t) = T(t)·S(t) + _t, (мультипликативная);

2. Регрессионные модели с одним уравнением

В таких моделях зависимая переменная y представляется в виде функции y = f(x₁,… , x_n), где x₁, … , x_n - независимые (объясняющие) переменные. В зависимости от вида функции f(x₁,… , x_n) модели делятся на линейные и нелинейные.

3. Системы одновременных уравнений

Эти модели описываются системами одновременных уравнений, которые могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы.

Примером системы одновременных уравнений является модель спроса и предложения, когда объем спроса на товар (Q^d) определяется его ценой (P) и доходом потребителя (I), объем предложения (Q^s) – его ценой (P) и достигается равновесие между спросом и предложением:

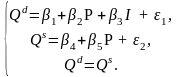
При математическом моделировании мы встречаемся с двумя типами данных: пространственные данные (набор показателей экономических переменных в один и тот же момент времени) и временные ряды (серия наблюдений одной и той же случайной величины в последовательные моменты времени).

Весь процесс математического моделирования можно разделить на шесть основных этапов:

• постановочный (на этом этапе формируется цель исследования, определяется набор участвующих в модели экономических переменных);

• априорный (проводится анализ экономической сущности изучаемого объекта, формирование и формализация известной до начала исследования (априорной) информации);

• параметризация (осуществляется непосредственно моделирование, т.е. выбор общего вида модели, в том числе состава переменных и формы их связи);

• информационный (собирается необходимая статистическая информация - наблюдаемые значения экономических переменных);

• идентификация модели (на .том этапе проводится статистический анализ модели и оценка ее параметров);

• верификация модели (проверяется истинность, адекватность модели, т.е. соответствие моделируемому реальному экономическому объекту).

На первых трех этапах весьма важной является проблема спецификации модели, включающая выражение в математической форме выявленных связей и соотношений, установление состава объясняющих переменных (в том числе и лаговых), формулировка исходных предпосылок и ограничений модели и ряд других вопросов. Спецификация опирается на имеющиеся экономические теории, специальные знания, а также на интуитивные представления об анализируемом экономическом объекте.

От проблемы идентификации модели (которая заключается в выборе и реализации методов статистического оценивания ее неизвестных параметров) следует отличать проблему ее идентифицируемости, т.е. проблему возможности получения однозначно определенных параметров модели, заданной системой одновременных уравнений.

Широкому внедрению эконометрических методов способствовало развитие информационных технологий. Компьютерные эконометрические пакеты сделали эти методы более доступными. Наиболее трудоемкая работа по вычислению различных статистик, параметров, построению таблиц и графиков в основном выполняется компьютером, а исследователю остается работа по постановке задачи, выбору соответствующей модели и метода ее решения, а также интерпретации результатов.