6.Повздовжні коливання стержня або поперечні коливання струни.
Задача. Знайти закон повздовжнього коливання тонкого пружного стержня, лівий кінець якого закріплений, а правий - вільний. Початковий розподіл переміщень вздовж стержня показано на малюнку 6.1.
0
Мал. 6.1
Функція
задана формулами
.
(6.1)
Початкова швидкість точок стержня дорівнює нулю:
.
(6.2)
Повздовжні коливання стержня описуються рівнянням
,
(6.3)
причому у відповідності з заданими граничними умовами
.
(6.4)
Таким чином задача зводиться до рішення диференціального рівняння (6.3) при граничних (6.4) і початкових (6.1) – (6.2) умовах.
Для зручності подальших викладок перейдемо до безрозмірних величин:
.
(6.5)
Якщо в умові задана початкова швидкість, то перехід до безрозмірного переміщення здійснюється за формулою
.
Враховуючи що
.
(6.6)
Рівняння (6.3) і умови (6.1), (6.2), (6.4) перепишемо у вигляді
,
(6.7)
(6.8)
.
(6.9)
Розв’язок рівняння (6.7)
.
(6.10)
Підставляючи (6.10) у (6.7), одержимо
,
(6.11)
.
Остання рівність можлива лише у тому випадку, коли обидві частини не залежать від і , тобто вони – постійні. Позначимо цю сталу через . Тоді з рівності (6.11) одержимо два звичайних диференціальних рівняння:
(6.12)
(6.13)
Розв’язав ці рівняння, і підставив висліди в (6.10), одержимо
,
(6.14)
де
- довільні сталі.
Одержали загальний розв’язок рівняння (6.7).
Для знаходження частинного розв’язку з граничних та початкових умов визначимо константи.
Застосовуючи першу граничну умову з здачі Штурма-Ліувіля, одержимо
(6.15)
Для
застосування другої
граничної умови
знайдемо частинну
похідну
Отже, власними функціями будуть
Підставляючи одержані результати в (6.10), знаходимо частинні розв’язки рівняння (6.7), які задовольняють крайовим умовам (6.9).
При цьому кожному
значенню
буде відповідати розв’язок
.
(6.16)
Сума розв’язків (6.16) також буде розв’язком рівняння (6.7), тому що (6.7) лінійне й однорідне:
,
(6.17)
Нехай
,
а
,
тоді формула (6.17) буде
,
(6.18)
Для визначення
констант
і
використаємо початкові умови (6.8).
Для застосування другої початкової умови знайдемо частинну похідну:
,
(6.19)
.
Одержали
;
тоді
.
(6.20)
Для знаходження використаємо останню початкову умову, з якої виходить
.
Остання
формула показує, що постійні – це
коефіцієнти розкладання функції
у ряд Фур’є за синусами
у проміжку
.
Таким чином,
.
Підставляючи вираз (6.8) для функції під інтеграл, одержуємо
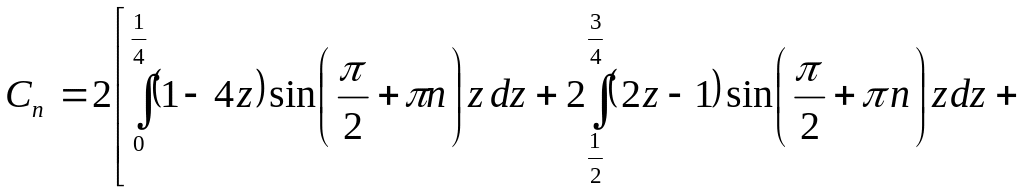
Зробивши необхідні обчислення, маємо
(6.21)
Підставляючи (6.21) у (6.20), запишемо остаточно розв’язок задачі
(6.22)
Зауваження.
Якщо початкова
швидкість
відмінна від нуля, то у формулі (6.19)
необхідно ввести позначення
(6.23)
Далі вираховуємо коефіцієнт ряду Фур’є
де
- початкова швидкість.
Для того, щоб підставити у формулу (6.18), треба скористатися співвідношенням
Нехай змінюється від 0 до 1 з кроком 0.2, а - від 0 до 1 з кроком 0.25.
Мал.6.2