3.2. Теплопроводность

Закон Фурье (1822 г.) является основным законом 'теплопроводности, устанавливающим прямую пропорциональность между поверхностной плотностью теплового потока и температурным градиентом:

(3.5)

где  – множитель пропорциональности, который называется коэффициентом теплопроводности, Вт/(мК).

Рис. 3.2. Распределение температур в однослойной плоской стенке	Рис. 3.3. Распределение температур в многослойной плоской стенке

Знак минус указывает, что вектор теплового потока направлен в сторону, противоположную температурному градиенту. Из уравнения (3.5) видно, что коэффициент теплопроводности количественно равен удельному тепловому потоку при температурном градиенте, равном единице (изменение температуры в 1°С на 1 м).

Коэффициент теплопроводности является важной теплофизической характеристикой вещества: чем больше , тем большей теплопроводностью обладает вещество. Коэффициент теплопроводности зависит от природы вещества, его структуры, влажности, наличия примесей, температуры и других факторов.

В практических расчетах коэффициент теплопроводности строительных материалов надлежит принимать по СНиП II-3-79** «Строительная теплотехника».

Рассмотрим однослойную плоскую стенку толщиной  (рис. 3.2), коэффициент теплопроводности которой постоянен и равен . Температуры на границах стенки t₁ и t₂, причем t₁>t₂. Теплота распространяется только вдоль оси х. При этих условиях температурное поле в стенке будет одномерным, изотермическими поверхностями будут плоскости, параллельные поверхностям стенки.

Для слоя толщиной dx на основании закона Фурье (3.5) можно написать следующие уравнения теплопроводности:

(3.6)

Проинтегрируем данное уравнение. После преобразования получаем:

(3.7)

(3.8)

Из уравнения видно, что поверхностная плотность теплового потока зависит от температурного перепада.

Отношение называется термическим сопротивлением стенки. Зная поверхностную плотность теплого потока q, можно определить общее количество теплоты, переданной за 1 ч через стенки поверхности F, по формуле:

Q=qF (3.9)

Из формулы (3.9) видно, что общее количество теплоты, переданной через однослойную плоскую стенку, пропорционально поверхностной плотности теплового потока и площади поверхности стенки.

Рассмотрим теплопроводность плоской многослойной стенки, состоящей из n материальных слоев, плотно прилегающих один к другому (рис. 3.3). Каждый слой имеет заданную толщину , и коэффициент теплопроводности . Многослойными являются, например, стены и перекрытия крупнопанельных и кирпичных зданий.

При стационарном тепловом режиме тепловые потоки, проходящие через каждый из слоев стенки, одинаковы. Тепловой поток можно определить по формуле (3.10).

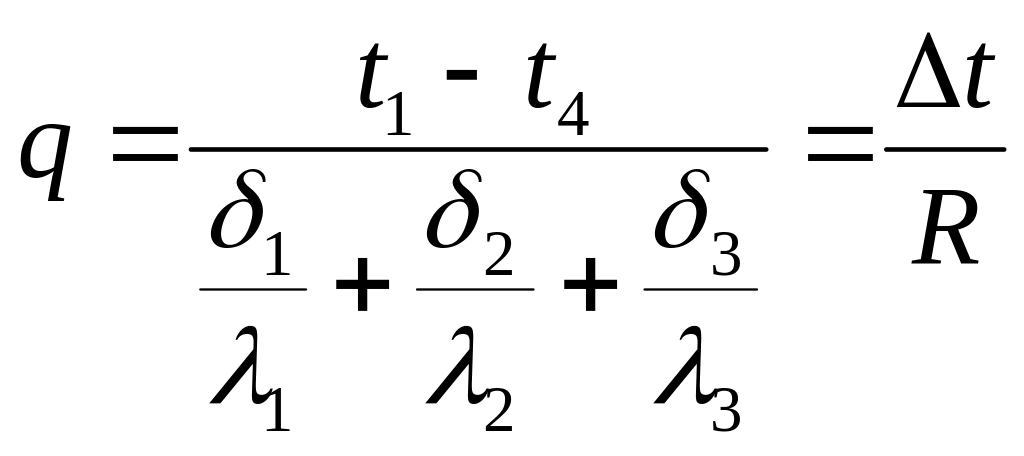(3.10)

3.3. Конвективный теплообмен

Тепловой поток Q, Вт, передаваемый при конвективном теплообмене, определяется по формуле Ньютона

(3.11)

где _к – коэффициент пропорциональности, называемый коэффициентом теплоотдачи; F – поверхность соприкосновения теплоносителя со стенкой, м²; t_ж –температура теплоносителя, °С; t_с – температура поверхности стенки, °С.

Приняв F = l м², получим поверхностную плотность теплового потока q, Вт/м²:

(3.12)

Коэффициент теплоотдачи () представляет собой количество теплоты, проходящей в единицу времени от жидкости (газа) к стенке (или наоборот) через 1 м² поверхности при разности температур жидкости и стенки 1°. Единица измерения Вт/(м²К). В отличие от коэффициента теплопроводности коэффициент теплоотдачи – очень сложная величина, которой учитываются следующие факторы, обусловливающие протекание конвективного теплообмена: характер движения жидкости или газа (ламинарное или турбулентное) и природа его возникновения; скорость движения жидкости или газа, физические параметры жидкости или газа (коэффициент теплопроводности, вязкость; плотность, теплоемкость, коэффициент объемного расширения), температура жидкости или газа и поверхности; форма и линейные размеры омываемой жидкостью или газом поверхности.

Для определения величины  для различных случаев конвективного теплообмена предложено несколько эмпирических формул, имеющих, однако, ограниченную область применения. Значительно лучшие результаты дает определение величины  на основе эксперимента с использованием критериев подобия–безразмерных соотношений параметров, характеризующих физический процесс.